Previous:
This post is about implementing a binary tree in C using an array. You can visit Binary Trees for the concepts behind binary trees. We will use array representation to make a binary tree in C and then we will implement inorder, preorder and postorder traversals in both the representations and then finish this post by making a function to calculate the height of the tree.
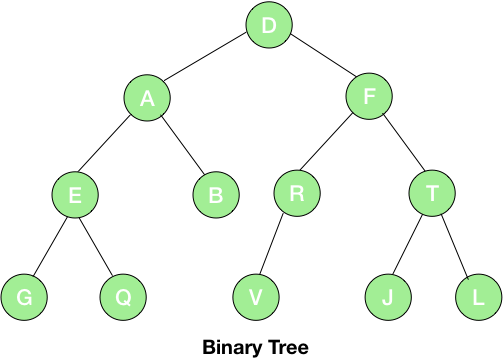
We will use the above tree for the array representation. As discussed in the post Binary Trees, the array we will use to represent the above tree will be:
| \0 | D | A | F | E | B | R | T | G | Q | \0 | \0 | V | \0 | J | L |
Let’s start with the first step and make an array.
#include <stdio.h>
/*
D
/ \
/ \
/ \
A F
/ \ / \
/ \ / \
E B R T
/ \ / / \
G Q V J L
*/
int complete_node = 15;
char tree[] = {'\0', 'D', 'A', 'F', 'E', 'B', 'R', 'T', 'G', 'Q', '\0', '\0', 'V', '\0', 'J', 'L'};
int main()
{
return 0;
}
int complete_node = 15 – It is just a variable to keep the total number of nodes if the tree given is a complete binary tree.
char tree[ ] – It is the array which is storing the entire binary tree.
Now, we are ready with a binary tree and the next step is to make the functions to traverse over this binary tree. But before doing so, we need two more functions to get the left and the right children of any node. So, let’s make these functions first.
Function to Get Right and Left Children
int get_right_child(int index)
{
if(tree[index]!='\0' && ((2*index)+1)<=complete_node)
return (2*index)+1;
return -1;
}
tree[index]!='\0' – Checking if the current node is not null.
(2*index)+1)<=complete_node – We know that the right child of node ‘i’ is given by (2*i)+1 but this value must lie within the number of elements in the array. And this condition checks the same.
return (2*index)+1 – If both the above conditions are satisfied then we are returning the index of the right child.
return -1 – In case of failure, we are returning -1, a negative value to represent failure.
Similarly, we can make a function to get the left child of the tree by using the property that the left child of node ‘i’ of a complete binary tree is given by 2*i.
int get_left_child(int index)
{
if(tree[index]!='\0' && (2*index)<=complete_node)
return 2*index;
return -1;
}
We are now ready with the functions. So, let’s make the functions to traverse the binary tree.
Traversals in Binary Tree
Preorder Traversal
void preorder(int index)
{
if(index>0 && tree[index]!='\0')
{
printf(" %c\n",tree[index]);
preorder(get_left_child(index));
preorder(get_right_child(index));
}
}
if(index>0 && tree[index]!='\0') – We are first checking if the index given is valid or not because the functions we made above to get the children of the tree return -1 for an invalid result so, the condition index>0 checks the same. The condition tree[index]!='\0' checks if the node is not null.
printf(" %c\n",tree[index]) – We are first visiting the root.
preorder(get_left_child(index)) – Then we are visiting the left child
preorder(get_right_child(index)) – And at last, the right child.
These are explained in the Binary Trees post.
Similarly, we can write functions for the postorder and inorder traversals.
Postorder Traversal
void postorder(int index)
{
if(index>0 && tree[index]!='\0')
{
postorder(get_left_child(index));
postorder(get_right_child(index));
printf(" %c\n",tree[index]);
}
}
Inorder Traversal
void inorder(int index)
{
if(index>0 && tree[index]!='\0')
{
inorder(get_left_child(index));
printf(" %c\n",tree[index]);
inorder(get_right_child(index));
}
}
Let’s test these function in the main function.
#include <stdio.h>
/*
D
/ \
/ \
/ \
A F
/ \ / \
/ \ / \
E B R T
/ \ / / \
G Q V J L
*/
// variable to store maximum number of nodes
int complete_node = 15;
// array to store the tree
char tree[] = {'\0', 'D', 'A', 'F', 'E', 'B', 'R', 'T', 'G', 'Q', '\0', '\0', 'V', '\0', 'J', 'L'};
int get_right_child(int index)
{
// node is not null
// and the result must lie within the number of nodes for a complete binary tree
if(tree[index]!='\0' && ((2*index)+1)<=complete_node)
return (2*index)+1;
// right child doesn't exist
return -1;
}
int get_left_child(int index)
{
// node is not null
// and the result must lie within the number of nodes for a complete binary tree
if(tree[index]!='\0' && (2*index)<=complete_node)
return 2*index;
// left child doesn't exist
return -1;
}
void preorder(int index)
{
// checking for valid index and null node
if(index>0 && tree[index]!='\0')
{
printf(" %c ",tree[index]); // visiting root
preorder(get_left_child(index)); //visiting left subtree
preorder(get_right_child(index)); //visiting right subtree
}
}
void postorder(int index)
{
// checking for valid index and null node
if(index>0 && tree[index]!='\0')
{
postorder(get_left_child(index)); //visiting left subtree
postorder(get_right_child(index)); //visiting right subtree
printf(" %c ",tree[index]); //visiting root
}
}
void inorder(int index)
{
// checking for valid index and null node
if(index>0 && tree[index]!='\0')
{
inorder(get_left_child(index)); //visiting left subtree
printf(" %c ",tree[index]); //visiting root
inorder(get_right_child(index)); // visiting right subtree
}
}
int main()
{
printf("Preorder:\n");
preorder(1);
printf("\nPostorder:\n");
postorder(1);
printf("\nInorder:\n");
inorder(1);
printf("\n");
return 0;
}
Output:
Preorder:
D A E G Q B F R V T J L
Postorder:
G Q E B A V R J L T F D
Inorder:
G E Q A B D V R F J T L
Function to Determine the Height of a Binary Tree
Before making this function, we need to make one more function to determine whether a node is a leaf or not. A node is a leaf if it doesn’t have any children. Thus in our array, a node can be a leaf if both the left and the right subtrees are null like node ‘B’ or if the indices returned by the functions get_left_child and get_right child are -1 which will be in the case of nodes ‘G’, ‘Q’, ‘V’, etc.
int is_leaf(int index)
{
// to check of the indices of the left and right children are valid or not
if(!get_left_child(index) && !get_right_child(index))
return 1;
// to check if both the children of the node are null or not
if(tree[get_left_child(index)]=='\0' && tree[get_right_child(index)]=='\0')
return 1;
return 0; // node is not a leaf
}
!get_left_child(index) && !get_right_child(index) – The condition will be true if both the conditions are false i.e., both the indices are non-positive meaning both the left child and the right child don’t exist and thus, the node is a leaf.
tree[get_left_child(index)]=='\0' && tree[get_right_child(index)]=='\0' – If the above case is not satisfied then we are still in the function and these conditions will check if both the children of a node are null or not. In this case also, the node will be a leaf.
return 0 – If neither of the above cases is satisfied then the node is a non-leaf node.
Let’s write the function to determine the height of a binary tree.
int get_max(int a, int b)
{
return (a>b) ? a : b;
}
The function given above just returns the maximum among two numbers.
int get_height(int index)
{
if(tree[index]=='\0' || index<=0 || is_leaf(index))
return 0;
return(get_max(get_height(get_left_child(index)), get_height(get_right_child(index)))+1);
}
if(tree[index]=='\0' || index<=0 || is_leaf(index)) – The height of a leaf is 0. Also, for the invalid cases, the height will be 0.
return(get_max(get_height(get_left_child(index)), get_height(get_right_child(index)))+1) – The height of a node will be 1+ maximum of the height of the left subtree and the height of the right subtree.
Using this in the main function:
#include <stdio.h>
/*
D
/ \
/ \
/ \
A F
/ \ / \
/ \ / \
E B R T
/ \ / / \
G Q V J L
*/
int complete_node = 15;
char tree[] = {'\0', 'D', 'A', 'F', 'E', 'B', 'R', 'T', 'G', 'Q', '\0', '\0', 'V', '\0', 'J', 'L'};
int get_right_child(int index)
{
// node is not null
// and the result must lie within the number of nodes for a complete binary tree
if(tree[index]!='\0' && ((2*index)+1)<=complete_node)
return (2*index)+1;
// right child doesn't exist
return -1;
}
int get_left_child(int index)
{
// node is not null
// and the result must lie within the number of nodes for a complete binary tree
if(tree[index]!='\0' && (2*index)<=complete_node)
return 2*index;
// left child doesn't exist
return -1;
}
int is_leaf(int index)
{
// to check of the indices of the left and right children are valid or not
if(!get_left_child(index) && !get_right_child(index))
return 1;
// to check if both the children of the node are null or not
if(tree[get_left_child(index)]=='\0' && tree[get_right_child(index)]=='\0')
return 1;
return 0; // node is not a leaf
}
int get_max(int a, int b)
{
return (a>b) ? a : b;
}
int get_height(int index)
{
// if the node is a leaf the the height will be 0
// the height will be 0 also for the invalid cases
if(tree[index]=='\0' || index<=0 || is_leaf(index))
return 0;
// height of node i is 1+ maximum among the height of left subtree and the height of right subtree
return(get_max(get_height(get_left_child(index)), get_height(get_right_child(index)))+1);
}
int main()
{
printf("%d\n",get_height(1));
return 0;
}
Output:
3
#include <stdio.h>
/*
D
/ \
/ \
/ \
A F
/ \ / \
/ \ / \
E B R T
/ \ / / \
G Q V J L
*/
int complete_node = 15;
char tree[] = {'\0', 'D', 'A', 'F', 'E', 'B', 'R', 'T', 'G', 'Q', '\0', '\0', 'V', '\0', 'J', 'L'};
// funtion to get parent
int get_parent(int index)
{
if(tree[index]!='\0' && index>1 && index<=complete_node) //root has no parent
return index/2;
return -1;
}
int get_right_child(int index)
{
// node is not null
// and the result must lie within the number of nodes for a complete binary tree
if(tree[index]!='\0' && ((2*index)+1)<=complete_node)
return (2*index)+1;
// right child doesn't exist
return -1;
}
int get_left_child(int index)
{
// node is not null
// and the result must lie within the number of nodes for a complete binary tree
if(tree[index]!='\0' && (2*index)<=complete_node)
return 2*index;
// left child doesn't exist
return -1;
}
void preorder(int index)
{
// checking for valid index and null node
if(index>0 && tree[index]!='\0')
{
printf(" %c ",tree[index]); // visiting root
preorder(get_left_child(index)); //visiting left subtree
preorder(get_right_child(index)); //visiting right subtree
}
}
void postorder(int index)
{
// checking for valid index and null node
if(index>0 && tree[index]!='\0')
{
postorder(get_left_child(index)); //visiting left subtree
postorder(get_right_child(index)); //visiting right subtree
printf(" %c ",tree[index]); //visiting root
}
}
void inorder(int index)
{
// checking for valid index and null node
if(index>0 && tree[index]!='\0')
{
inorder(get_left_child(index)); //visiting left subtree
printf(" %c ",tree[index]); //visiting root
inorder(get_right_child(index)); // visiting right subtree
}
}
int is_leaf(int index)
{
// to check of the indices of the left and right children are valid or not
if(!get_left_child(index) && !get_right_child(index))
return 1;
// to check if both the children of the node are null or not
if(tree[get_left_child(index)]=='\0' && tree[get_right_child(index)]=='\0')
return 1;
return 0; // node is not a leaf
}
int get_max(int a, int b)
{
return (a>b) ? a : b;
}
int get_height(int index)
{
// if the node is a leaf the the height will be 0
// the height will be 0 also for the invalid cases
if(tree[index]=='\0' || index<=0 || is_leaf(index))
return 0;
// height of node i is 1+ maximum among the height of left subtree and the height of right subtree
return(get_max(get_height(get_left_child(index)), get_height(get_right_child(index)))+1);
}