Previous
A binary tree is a tree in which every node has at most 2 children i.e., the left child and the right child.
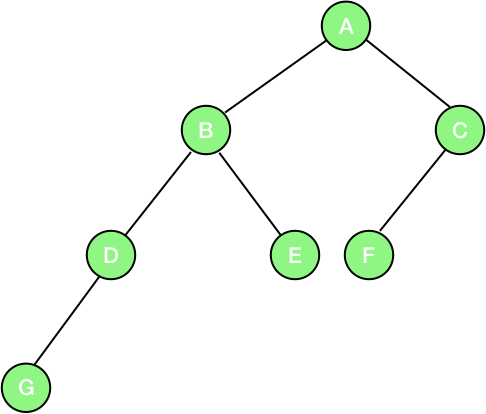
For example, in the above picture, the node ‘B’ has 2 children, node ‘D’ has 1 child and node ‘G’ has 0 children. Since every node has at most 2 children, so the tree is a binary tree.
There are also different types of binary trees which are listed below:
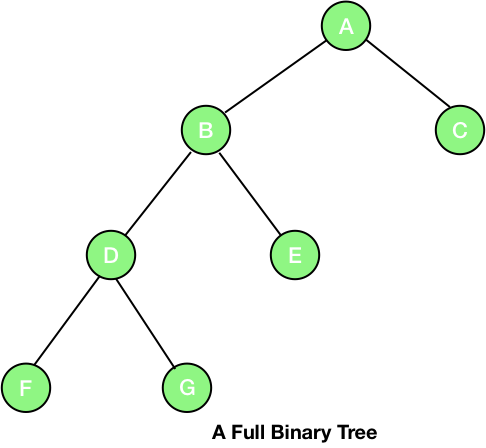
Full Binary Tree - A binary tree in which every node has 2 children except the leaves is known as a full binary tree.
Complete Binary Tree - A binary tree which is completely filled with a possible exception at the bottom level i.e., the last level may not be completely filled and the bottom level is filled from left to right.
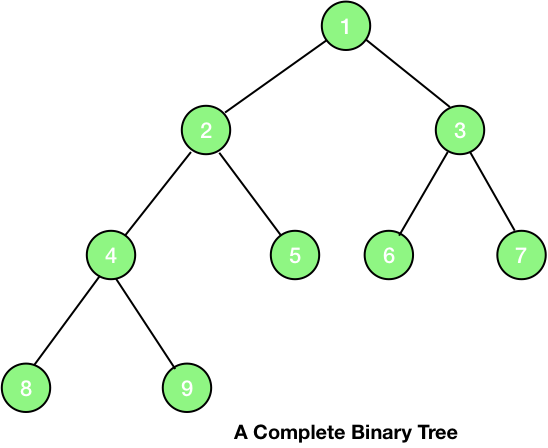
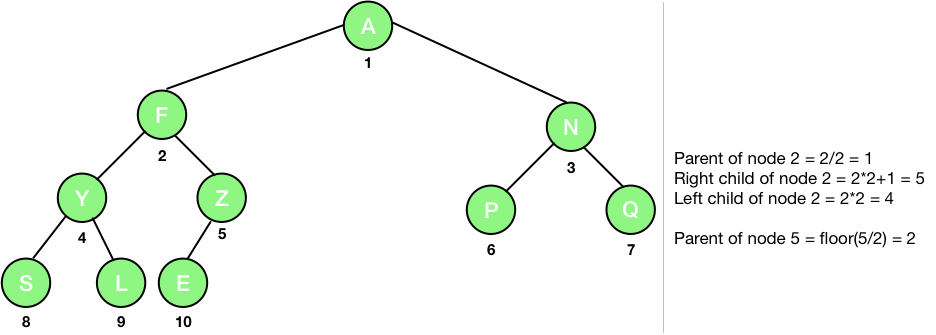
As you can see in the picture given above, the numbering of the nodes starts from 1 and assigned from top to bottom and left to right at the same level.
There are few very useful properties of a complete binary tree which are given below:
- The parent of node i is floor function of i/2, except the root node which has no parent. For example, the parent of the node 2 is 2/2 i.e., the node 1 and the parent of the node 3 is also node 1 (floor function of 3/2).
- The left child of the node i is 2i, if the left child exists i.e., 2i > the total number of nodes. For example, the left child of the node 4 is 2*4 i.e., the node 8.
- The right child of the node i is 2i+1, if the right child exists i.e., 2i+1 > the total number of nodes. For example, the left child of node 4 is 2*4 + 1 i.e., the node 9.
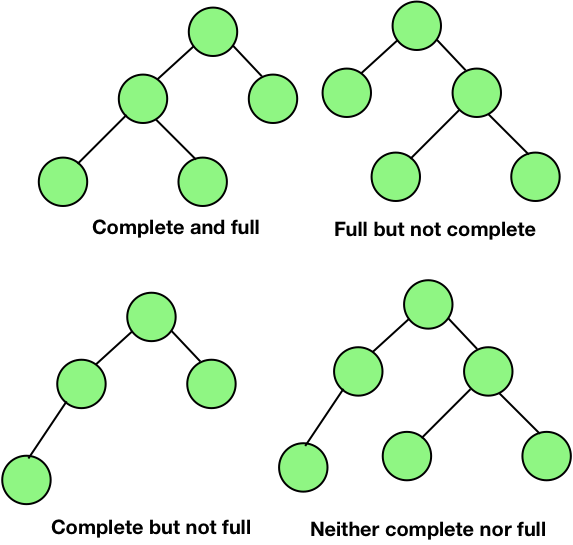
The picture given below clearly distinguishes between a complete binary tree and a full binary tree.
Perfect Binary Tree - In a perfect binary tree, each leaf is at the same level and the and all the interior nodes have two children. It means that a perfect binary tree of height h has exactly 2h+1-1 nodes.
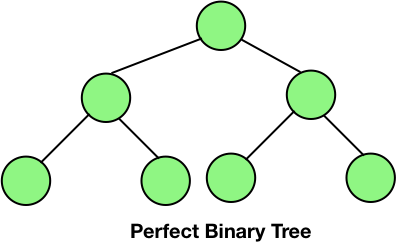
Maximum Number of Nodes in a Binary Tree (Nodes in Perfect Binary Tree)
Let’s take a perfect binary tree of height h.
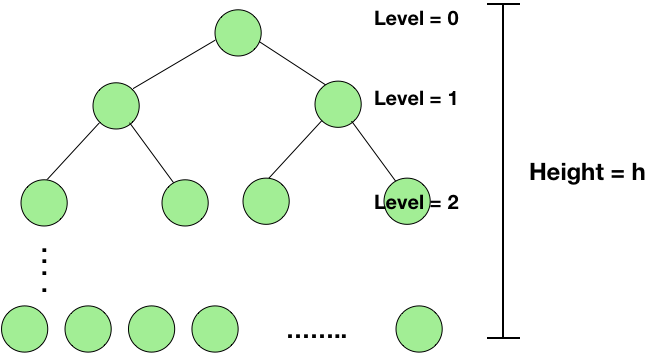
Number of nodes at level 0 = 20 = 1
Number of nodes at level 1 = 21 = 2
Similarly, number of nodes at level h = 2h
Total number of nodes = 20 + 21 + ….. + 2h = 2h+1-1.
Therefore, the total number of nodes = 2h+1-1.
Also, 2h+1-1 = 2*2h-1
Let the total number of nodes = n
=> n = 2*2h-1
=> 2h = (n+1)/2
=> h = log((n+1)/2)
Note that the base of the log here is 2.
From the equation, one can also say that the number of leaves in a perfect binary tree is 2h and thus the total number of non-leaf nodes is 2h+1-1-2h = 2h-1 i.e., the number of leaf nodes - 1.
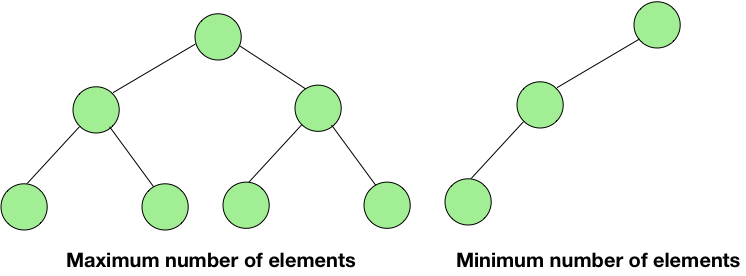
Also, the maximum number of nodes of a binary tree of height h can have is 2h+1-1 i.e., the case when the tree is a perfect binary tree and the minimum number of nodes a binary tree of height h can have is when the tree is linear i.e., h+1.
Representations of a Binary Tree
We can represent a binary tree in two way:
- Array representation
- Linked representation
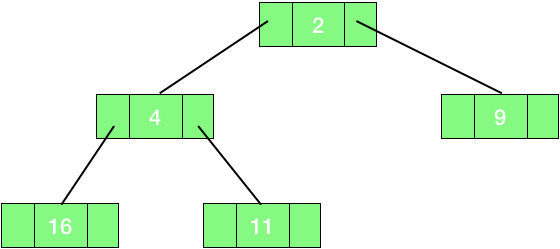
Array Representation of Binary Tree
A binary tree can be stored in a single array. We number the nodes from top to bottom, and from left to right for the nodes at the same level. Then the values at the nodes are stored in an array with the index corresponding to the numbers given to the nodes. This is shown in the figure given below.
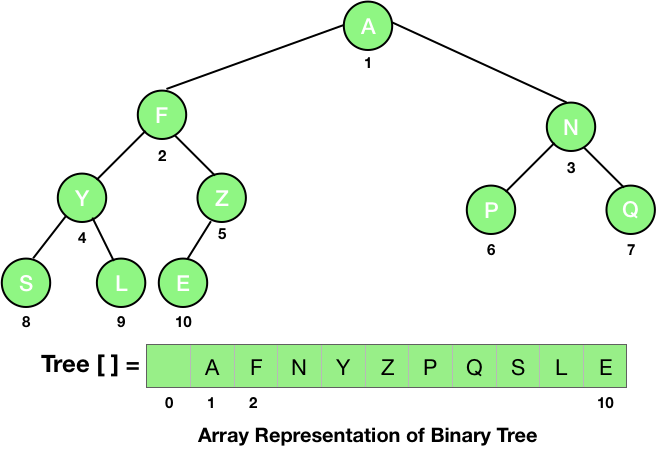
You can see that we start filling the array from the index 1 and the element at the index 0 is left empty or null.
For an incomplete tree, we first assume that there are nodes present to make the tree a complete tree and then number the nodes as shown in the figure given below.
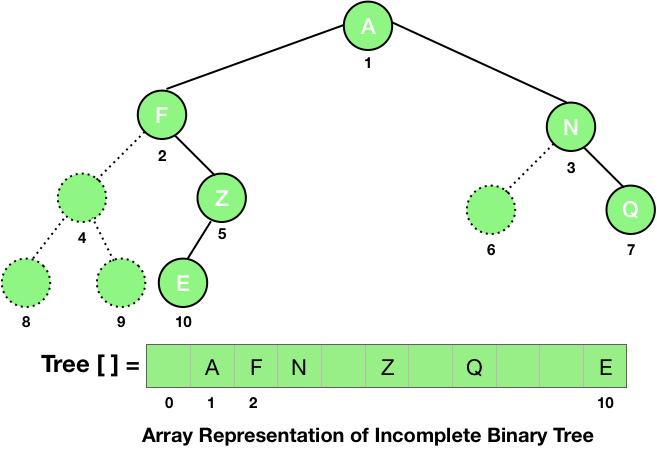
From the properties of a complete binary tree, we can easily calculate the parent, the left child and the right child of a node at index i as floor of i/2, 2*i and 2*i+1.
Linked Representation of a Binary Tree
As discussed in the Trees in Computer Science, in the linked representation, the node contains mainly three elements, the data to store, a link to the left child, and a link to the right child. It is shown in the figure given below.
The pseudo code is given below. However, you can visit Binary Tree in C: Linked Representation & Traversals, Binary Trees in C : Array Representation and Traversals and Binary Tree in Java: Traversals, Finding Height of Node for full programmatic representations of a binary tree in C and Java.
class Node
{
String data;
Node left;
Node right;
}
Traversal of a Binary Tree
Traversal is a systematic way of visiting or accessing every node of a tree. The three basic types of traversals are:
- Preorder
- Inorder
- Postorder
Preorder Traversal
In this traversal, the root of the tree is visited first and then the left subtree and finally the right subtree. So, we can write the programmatic representation of preorder traversal as:
function preorder(Node n):
{
if(n != null)
{
print(n.data) // Printing the data at the root
preorder(n.left) // Visiting the left subtree
preorder(n.right) // Visiting the right subtree
}
}
print(n.data) – We are first printing the data at the node i.e., we are first visiting the root.
preorder(n.left) – After visiting the root, we are visiting the left subtree.
preorder(n.right) – And lastly the right subtree.
Let's consider an example of preorder traversal.
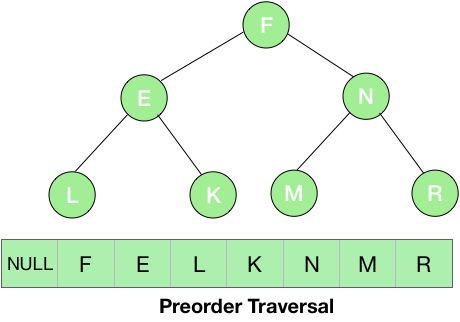
In the above example, we first visited the root i.e., the node F and printed it and then its left subtree. The root of the left subtree is E, so the next element to be printed is E and then again we visited the left subtree of this node which is L. L doesn’t have any children so, now we moved to its parent E. As there is no more element in the left subtree, we visited the right subtree i.e., K. Now, we have traversed the entire left part of F, so now its time for the right subtree N. We first printed the root of this subtree i.e., N and then moved to the left subtree i.e., M and then the right part i.e., R.
Inorder Traversal
In this traversal, the left subtree is visited first, then the root and finally the right subtree. The programmatic representation of the inorder traversal can be written as:
function inorder(Node n)
{
if(n != null)
{
inorder(n.left)
print(n.data)
inorder(n.right)
}
}
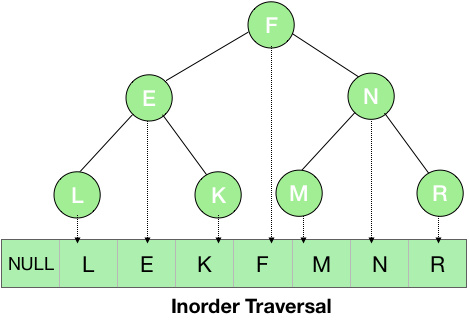
From the root of the tree i.e., node F, we first visited the left subtree – E and then its left subtree – L. Now, since there is no further left part of this subtree, thus we printed the root element i.e., L. For the subtree with root E, we have visited its left part thus printed its root i.e., node E and then moved to the right subtree – K. For the subtree K, there is no left part so, printed its root – K and then it also doesn’ t have any right child so, this subtree is complete. Now, the entire left part of the node F is completed thus we printed the root – F and then moved to its right subtree and then similarly printed M, N and R.
Postorder Traversal
In this traversal, the left subtree is visited first, then the right subtree and lastly the root. The pseudo code for the same can be written as:
function postorder(Node n)
{
if(n != null)
{
postorder(n.left)
postorder(n.right)
print(n.data)
}
}
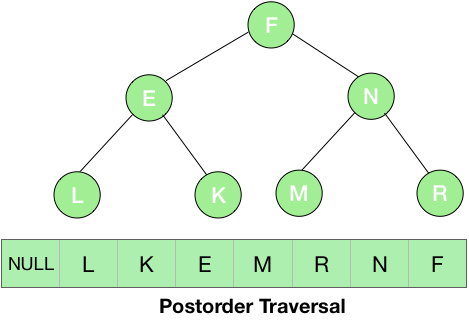
Here, we first visited the left subtree and then right and the root at last. So, we first printed L, then the right subtree K and lastly the root E for the left subtree of node F. Now, we will proceed to the right subtree and at last print the root F. Thus, we visited the node N and printed its left subtree – M then its right – R and lastly the root N. Now, we have visited both the left and the right subtrees of the node F thus, we printed the root N.
Now, you are ready with the concept of binary trees. You can visit these articles for the full coding implementation of the binary tree in C and Java:
Binary Trees in C : Array Representation and Traversals
Binary Tree in C: Linked Representation & Traversals
Binary Tree in Java: Traversals, Finding Height of Node







