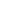Linked list is one of the most important data structures. We often face situations, where the data is dynamic in nature and number of data can’t be predicted or the number of data keeps changing during program execution. Linked lists are very useful in this type of situations.
The implementation of a linked list in C++ is done using pointers. You can go through the pointers chapter if you don’t have a strong grip over it. You can also practice a good number of questions from practice section.
A linked list is made up of many nodes which are connected in nature. Every node is mainly divided into two parts, one part holds the data and the other part is connected to a different node. It is similar to the picture given below.
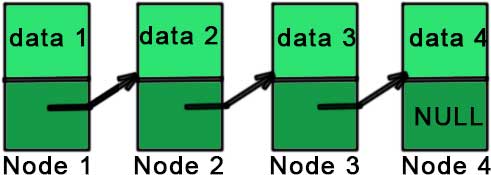
Here, each node contains a data member (the upper part of the picture) and link to another node(lower part of the picture).
Notice that the last node doesn’t point to any other node and just stores NULL.
In C++, we achieve this functionality by using structures and pointers. Each structure represents a node having some data and also a pointer to another structure of the same kind. This pointer holds the address of the next node and creates the link between two nodes. So, the structure is something like:
struct node
{
int data;
struct node *next;
};
The first data member of the structure (named node) is an integer to hold an integer and the second data member is the pointer to a node (same structure). This means that the second data member holds the address of the next node and in this way, every node is connected as represented in the picture above.
The picture representing the above structure is given below.
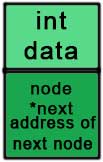
And the picture representing the linked list is:
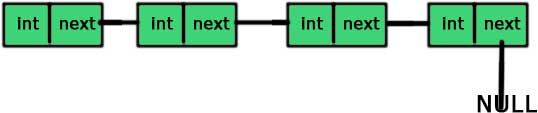
So, if we have access to the first node then we can access any node of the linked list. For example, if ‘a’ is a node then a->next is the node next to the ‘a’ (the pointer storing the address of the next node is named ‘next’).
One thing you should notice here is that we can easily access the next node but there is no way of accessing the previous node and this is the limitation of singly linked list.
Coding up a linked list
You are now clear with the concepts of a linked list. Let’s code it up. The first part is to create a node (structure).
#include <iostream>
using namespace std;
struct node
{
int data;
node *next;
};
Now, we will create a class ‘linked_list’ which will contain all the functions and data members required for a linked list. This class will use the structure ‘node’ for the creation of the linked list.
The second and the most important part of a linked list is to always keep the track of the first node because access to the first node means access to the entire list. So, let’s call our first node as ‘ head’.
#include <iostream>
using namespace std;
struct node
{
int data;
node *next;
};
class linked_list
{
private:
node *head,*tail;
public:
linked_list()
{
head = NULL;
tail = NULL;
}
};
int main()
{
linked_list a;
return 0;
}
We have made two nodes – head and tail. We will store the first node in ‘head’ and the last node in ‘tail’. The constructor of the linked list is making both ‘head ’ and ‘ tail’ NULL because we have not yet added any element to our linked list and thus both are NULL.
Now, let’s create a function of adding a node to our linked list.
#include <iostream>
using namespace std;
struct node
{
int data;
node *next;
};
class linked_list
{
private:
node *head,*tail;
public:
linked_list()
{
head = NULL;
tail = NULL;
}
void add_node(int n)
{
node *tmp = new node;
tmp->data = n;
tmp->next = NULL;
if(head == NULL)
{
head = tmp;
tail = tmp;
}
else
{
tail->next = tmp;
tail = tail->next;
}
}
};
int main()
{
linked_list a;
a.add_node(1);
a.add_node(2);
return 0;
}
If you are not familiar with the ‘malloc’ function, then just read the dynamic memory allocation chapter.
node *tmp=new node – We are allocating the space required for a node by the new operator. Now, ‘tmp’ points to a node (or space allocated for the node).
tmp->data = n – We are giving a value to the ‘data’ of ‘tmp’ as passed to the function.
tmp->next=NULL – We have given the value to ‘data’ in the previous line and a value of the pointer ‘next’ (NULL) in this line and thus making our node ‘tmp’ complete.
The next part after the creation of a node is to join the nodes and create the linked list. We will first check if the ‘head’ is NULL or not. If the ‘head’ is NULL, it means that there is no linked list yet and our current node(tmp) will be the ‘head’.
if(head == NULL)
{
head = tmp;
tail = tmp;
}
If ‘head’ is NULL, our current node (tmp) is the first node of the linked list and this it will be ‘head’ and ‘tail’ both (as it is also the last element right now).
If ‘head’ is not NULL, it means that we have a linked list and we just have to add the node at the end of the linked list.
else
{
tail->next = tmp;
tail = tail->next;
}
The new node (tmp) will go after the ‘tail’ and then we are changing the tail because the new node is the new ‘tail’.
Try to understand the code by allocating two to three nodes by above mechanism and you will get it.