Detect a Loop in a Linked List

Given a singly Linked List, detect if it contains a loop or not.

Input:

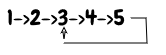
Output: True

Input: 1→ 2→ 3→ NULL
Output: False

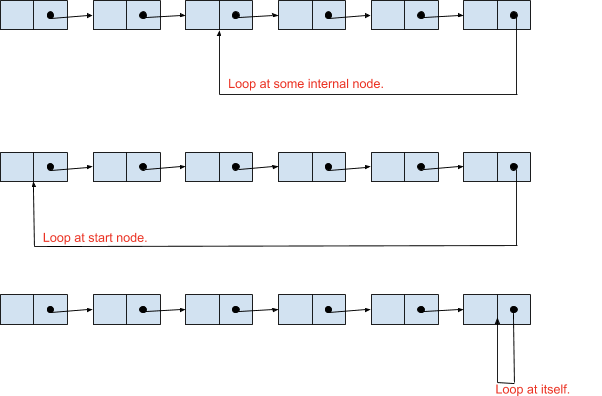
Generally, the last node of the Linked List points to a NULL pointer, which indicates the end of the Linked List. But in Linked List containing a loop, the last node of the Linked List points to some internal node/ start node/ itself. So in such cases, we need to detect and remove the loop by assigning next pointer of last node to NULL. This section explains about the detection part of the loop in a Linked List.

Check below figure to visualize a Linked List containing a loop.

Brute Force Approach

In the Brute Force Approach, we will use two nested loops. The inner loop will traverse the entire Linked List from the start node until the count of the number of nodes the outer loop has traversed, and will check if there is any node pointed by the inner loop that is equal to the node pointed by the outer loop. If it is, then a loop in the linked list exists.

Let’s derive exactly at which node the inner and outer loop will meet if there is a loop in the linked list. So consider a Linked List having length n. Now, imagine that the outer loop has traversed the entire list once and it is at the start node of the loop i.e. total n nodes traveled from the head node as you can see in the figure.

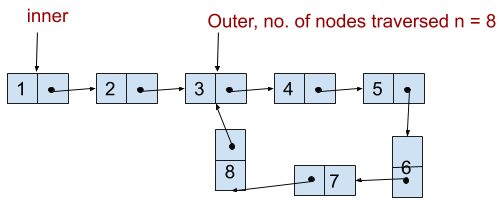
Therefore, the inner loop will always encounter the node pointed by the outer loop (i.e. start node of the loop) before traversing n nodes.

The time complexity of the brute force approach is $O(n^2)$.

Implementation of Brute force approach is shown below,

• C/C++
• Python
• Java

#include <stdio.h>
#include <stdlib.h>

// Definition for singly-linked list.
struct ListNode
{
    int val;
    struct ListNode *next;
};

int detectLoop(struct ListNode *head)
{
    struct ListNode *outer = head;
    int nodesTraversedByOuter = 0;
    // Traverse the Linked List.
    while (outer != NULL)
    {
        outer = outer->next;
        nodesTraversedByOuter++;
        struct ListNode *inner = head;
        int k = nodesTraversedByOuter;
        // iterating inner loop from head to number of nodes traversed by outer at this point.
        while (k > 0)
        {
            if (inner == outer)
            {
                return 1;
            }
            inner = inner->next;
            k--;
        }
    }
    return 0;
}

int main()
{
    struct ListNode *head = malloc(sizeof(struct ListNode));
    head->val = 2;
    struct ListNode *l1 = malloc(sizeof(struct ListNode));
    l1->val = 8;
    head->next = l1;
    struct ListNode *l2 = malloc(sizeof(struct ListNode));
    l2->val = 3;
    l1->next = l2;
    struct ListNode *l3 = malloc(sizeof(struct ListNode));
    l3->val = 5;
    l2->next = l3;
    struct ListNode *l4 = malloc(sizeof(struct ListNode));
    l4->val = 10;
    l3->next = l4;
    l4->next = l2;
    // 2->8->3->5->10--
    //      ^            |
    //      |             |
    //      |_ _ __ _|
    printf("%d", detectLoop(head));
    return 0;
}

class ListNode:
    def __init__(self, val):
        self.val = val
        self.next = None


def detectLoop(head):
    outer = head
    nodesTraversedByOuter = 0
    while outer != None:
        outer = outer.next
        nodesTraversedByOuter += 1
        k = nodesTraversedByOuter
        inner = head
        # iterating inner loop from head to number of nodes traversed by outer at this point.
        while k > 0:
            if outer == inner:
                return True
            inner = inner.next
            k -= 1
    return False


if __name__ == "__main__":
    head = ListNode(2)
    head.next = l1 = ListNode(8)
    l1.next = l2 = ListNode(3)
    l2.next = l3 = ListNode(5)
    l3.next = l4 = ListNode(10)
    l4.next = l2
    # 2->8->3->5->10--
    #   	^       	|
    #   	|       	|
    #   	---------
    print(detectLoop(head))

// Definition for singly-linked list.
class ListNode {
  int val;
  ListNode next;

  ListNode(int x) {
    val = x;
    next = null;
  }
}

public class Solution {
  public static void main(String args[]) {
    ListNode head = new ListNode(2);
    ListNode l1 = new ListNode(8);
    head.next = l1;
    ListNode l2 = new ListNode(3);
    l1.next = l2;
    ListNode l3 = new ListNode(5);
    l2.next = l3;
    ListNode l4 = new ListNode(10);
    l3.next = l4;
    l4.next = l2;
    // 2->8->3->5->10--
    // ^              |
    // |.             |
    // ---------
    System.out.println(new Solution().detectLoop(head));
  }

  public boolean detectLoop(ListNode head) {
    ListNode outer = head;
    int nodesTraversedByOuter = 0;
    // Traverse the Linked List.
    while (outer != null) {
      outer = outer.next;
      nodesTraversedByOuter++;
      ListNode inner = head;
      int k = nodesTraversedByOuter;
      // iterating inner loop from head to number of nodes traversed by outer at this
      // point.
      while (k > 0) {
        if (inner == outer) {
          return true;
        }
        inner = inner.next;
        k--;
      }
    }
    return false;
  }
}

Using Hashing

The simplest approach is to use hashing. Here, we traverse the list one by one while storing the node addresses in a hash table. So at any point, if we encounter the next address of the current node already present in the hash table, then there is a loop. Else if we encounter NULL (i.e., we reach the end of the Linked List), then there is no loop in the Linked List.

The average time and space complexity of the hashing approach is $O(n)$. However, reader should take note that in case of collision in hashing, the overall time complexity will depend on the implementation of the inbuilt Hashing DataStructure in the programming language. For example, in Java8, the complexity of HashSet in case of collision is $O(\log{n})$ which makes the time complexity of the entire process in order of $O(n\log{n})$.

Find below the implementation of the above approach,

• C/C++
• Python
• Java

#include <stdio.h>
#include <bits/stdc++.h>

using namespace std;

// Definition for singly-linked list.
struct ListNode
{
    int val;
    struct ListNode *next;
};

bool detectLoop(struct ListNode *ptr)
{
    unordered_set<ListNode *> s;
    while (ptr != NULL)
    {
        if (s.find(ptr) != s.end())
            return true;
        s.insert(ptr);
        ptr = ptr->next;
    }

    return false;
}

int main()
{
    struct ListNode *head = new ListNode;
    head->val = 2;
    struct ListNode *l1 = new ListNode;
    l1->val = 8;
    head->next = l1;
    struct ListNode *l2 = new ListNode;
    l2->val = 3;
    l1->next = l2;
    struct ListNode *l3 = new ListNode;
    l3->val = 5;
    l2->next = l3;
    struct ListNode *l4 = new ListNode;
    l4->val = 10;
    l3->next = l4;
    l4->next = l2;

    // 2->8->3->5->10--
    //       ^            |
    //       |             |
    //       |_ _ __ _|
    printf("%d", detectLoop(head));
    return 0;
}

class ListNode:
    def __init__(self, val):
        self.val = val
        self.next = None


def detectLoop(head):
    # Using set for hashtable.
    hashtable = set()
    ptr = head
    while ptr != None:
        # Check if node address already present.
        if ptr in hashtable:
            return True
        # Add the current node address to hashtable.
        hashtable.add(ptr)
        ptr = ptr.next
    return False


if __name__ == "__main__":
    head = ListNode(2)
    head.next = l1 = ListNode(8)
    l1.next = l2 = ListNode(3)
    l2.next = l3 = ListNode(5)
    l3.next = l4 = ListNode(10)
    l4.next = l2
    # 2->8->3->5->10--
    #   	^    	|
    #   	|    	|
    #   	---------
    print(detectLoop(head))

import java.util.HashSet;

// Definition for singly-linked list.
class ListNode {
  int val;
  ListNode next;

  ListNode(int x) {
    val = x;
    next = null;
  }
}

public class Solution {
  public static void main(String args[]) {
    ListNode head = new ListNode(2);
    ListNode l1 = new ListNode(8);
    head.next = l1;
    ListNode l2 = new ListNode(3);
    l1.next = l2;
    ListNode l3 = new ListNode(5);
    l2.next = l3;
    ListNode l4 = new ListNode(10);
    l3.next = l4;
    l4.next = l2;

    // 2->8->3->5->10--
    // ^               |
    // |                |
    // |________|
    System.out.println(new Solution().detectLoop(head));
  }

  public boolean detectLoop(ListNode head) {
    ListNode ptr1 = head;
    HashSet<ListNode> h = new HashSet<>();
    // Traverse the Linked List.
    while (ptr1 != null) {
      // Check if node address already present.
      if (h.contains(ptr1))
        return true;
      // Add the current node address to hashset
      h.add(ptr1);
      ptr1 = ptr1.next;
    }
    // If ptr1 reaches to None, then there is no loop. Hence return False.
    return false;
  }
}

Using Floyd’s Cycle Detection Algorithm

This approach uses slow and faster pointer technique by Floyd to detect a loop in the Linked List having $O(n)$ time complexity and $O(1)$ auxiliary space,

And the same is discussed in detail here.