This post is just an introduction to the divide and conquer algorithm. The main algorithms based on this will be discussed in the further posts.
As the name suggests, divide and conquer algorithm first divides the problem and then solves it. So, it is a recursive algorithm which first breaks the problem into sub-problems until the subproblems are simple enough to be solved directly (mainly using brute force) called base case. It is mainly a three-step process. The steps involved are:
Step 1 → Divide the problem into smaller subproblems. For example, if you have an array, then we approach the problem by breaking the array into further smaller sub-arrays.
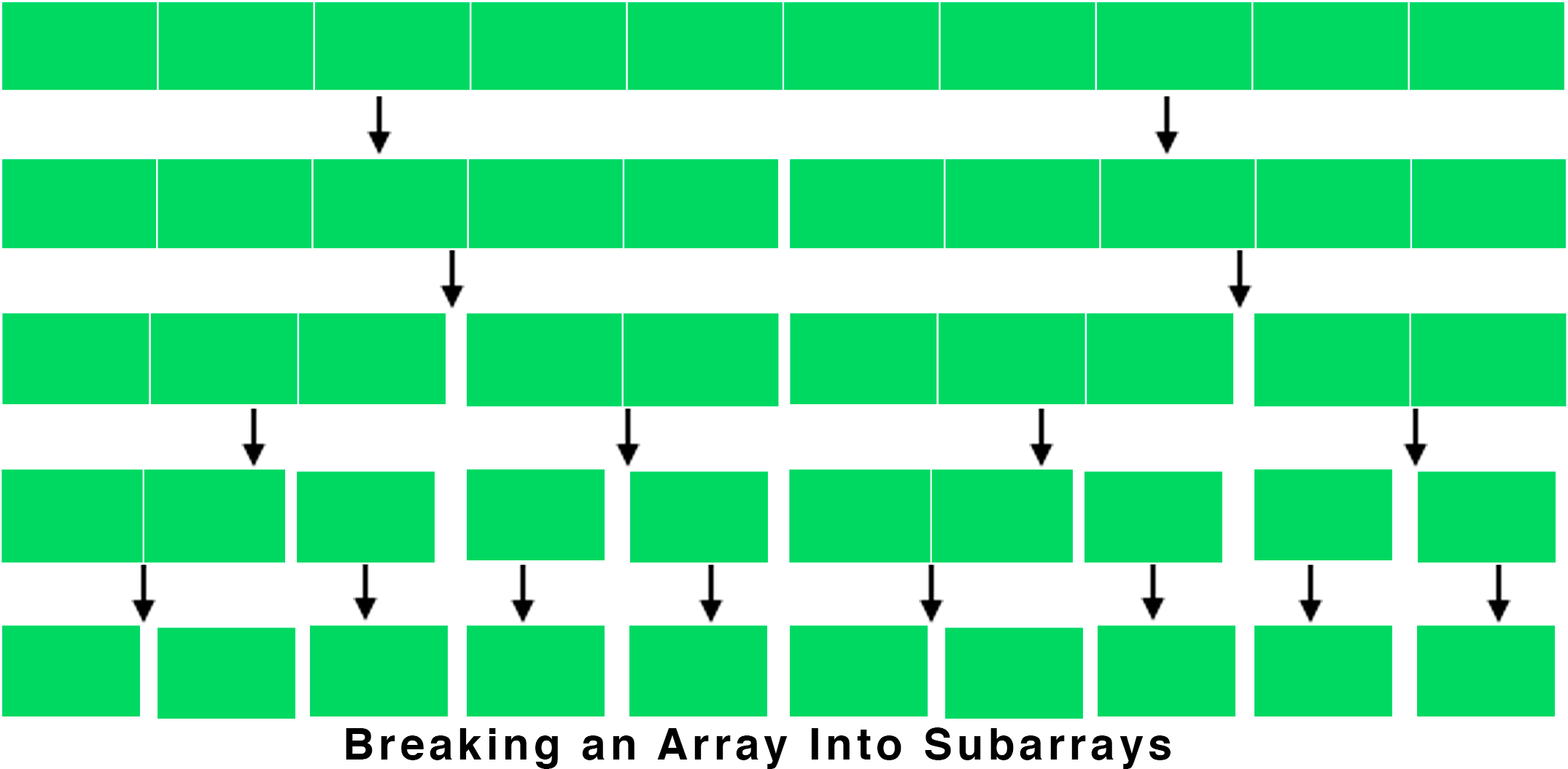
Step 2 → The second step is to solve the smaller subproblems. For example, if we have to search for an element in an array, then we will now search for the number in the smaller sub-arrays.
Step 3 → The third and the last step is to combine the subproblems to get the solution to the bigger problem. For example, let's consider a sorting problem. If all the sub-arrays are sorted, then it would be easy for us to get sort the main problem by combing the smaller sub-arrays.
So, we use divide and conquer when the problem is easy to divide into further subproblems and the subproblems are easy to solve.
Use of Divide and Conquer
Many algorithms are based on divide and conquer. I have only mentioned some of them in the list given below. I will discuss each of these in detail in my upcoming posts.
-
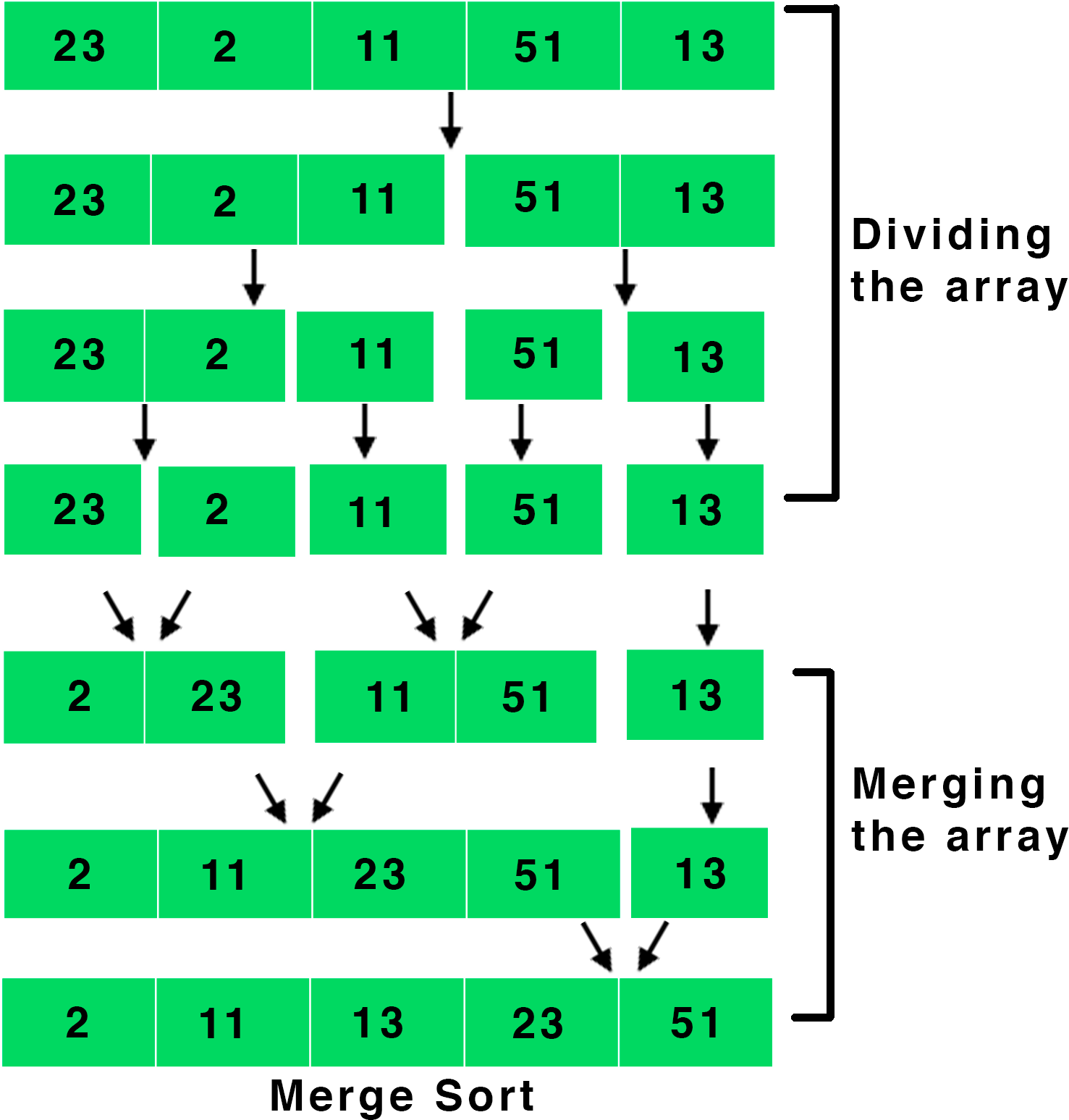
Merge Sort - It is a sorting algorithm which first breaks an array into smaller arrays and then recursively sorts and merges them. The pictorial representation is given below.
-
Quicksort - It is a technique in which a pivot is chosen and then all the elements smaller than the pivot are moved on one side of the array and all the elements bigger than the pivot are moved to another side. This is then repeated recursively for the subarrays.

-
Binary Search - It is an algorithm to search for an element in a sorted array. We first look at the middle element of the array and if the element matches then it is returned, otherwise if it is smaller, then we search in the left subarray, else in the right subarray.

- Karatsuba Algorithm - It is an algorithm of fast-multiplying two numbers efficiently. I will discuss the detail in an upcoming post.
- Closest Pair of Points - The closest pair of points is a problem in which we are given a set of points in XY plane and we have to find a pair of points with the least distance. The time complexity of the Brute Force solution is O(n2) i.e., nC2 but we can solve it in O(nlogn) with divide and conquer. We first sort the points to their x-coordinates and then divide the set into two parts and recursively solve both.







