Longest common subsequence

Problem explanation :  

Let’s understand the terms one by one,

Subsequence :  

A subsequence is a sequence which can be obtained from an array by removing some or no elements, without changing the order of elements.  

Common subsequence :  

We will be given two strings S of length N and T of length M, and we will say that C is a common subsequence of both the strings if it appears as a subsequence in both of the strings. We have to find the length of the longest such sequence.

Let’s understand with some examples,

S= abcde

T= acek

Following subsequences are common to both the strings :
‘a’
‘c’
‘e’
‘ac’
‘ae’
‘ce’
‘ace’

Longest subsequence which is common : ‘ace’

Solution:

One naive approach would be to generate all subsequences of string T and string S and find the longest matching subsequence.

We know that, for a string of length K, there are $2^K$ possible subsequences. So ,

Complexity : $O( 2 ^ {(max( N, M)} )$

Above approach can be implemented using recursion. We will write the recursive function as follows :

• Let’s define a function lcs( S, T , i, j ) as the length of the longest common subsequence of strings S and T. Initially, i=0 and j=0
• Now there are two cases :

1. If the current characters of both the sequences match, then we will check the next characters of both the sequences and add 1 to the length (lcs).
2. Else two recursive calls will be made, one for checking the current character of the string S with the next character of the string T and other for checking the current character of the string T with the next character of the string S and add the length of the maximum value of both the calls to lcs.

This step generates two different subsequences for each call.

Pseudocode for the above approach:

lcs( S, T , i, j )

    if there are no more characters in either of the string, return 0.

    else if the current characters of both the strings are equal
     return 1 + ( call for the next characters in both the strings )

    else ( 2 recursive calls will be made )
1. check the current character of string S with the next character of string T
2. check the current character of string T with the next character of string S
            add the maximum value of both the calls.

Implementation of the above approach:

• C/C++
• Python

// Recursive implementation of
// Longest Common subsequence problem

#include <bits/stdc++.h>
using namespace std;

int N, M;

// For calculating length of longest common subsequence

int lcs(string S, string T, int i, int j)
{
    // one or both of the strings are fully traversed

    if (i == N || j == M)
        return 0;

    // check if current characters are equal

    if (S[i] == T[j])
        // check for next character
        return (lcs(S, T, i + 1, j + 1) + 1);
    else
        // check which call has maximum value and add to length
        return max(lcs(S, T, i + 1, j), lcs(S, T, i, j + 1));
}

// Driver Code
int main()
{
    string S = " abcde";
    string T = "acek";

    N = S.length();
    M = T.length();
    cout << "Length of longest common subsequence " << lcs(S, T, 0, 0);

    return 0;
}

# Recursive implementation of
# Longest Common subsequence problem

# For calculating length of longest common subsequence

N = 0
M = 0


def lcs(S, T, i, j):

    # one or both of the strings are fully traversed

    if i == N or j == M:
        return 0

    # check if current character is equal

    if S[i] == T[j]:

        # check for next character

        return lcs(S, T, i + 1, j + 1) + 1
    else:

        # check which call has maximum value and add to length

        return max(lcs(S, T, i, j + 1), lcs(S, T, i + 1, j))


# Driver Code

S = "abcde"
T = "acek"

N = len(S)
M = len(T)

print("Length of longest common subsequence", lcs(S, T, int(0), int(0)))

Efficient approach using Memoization:

The above approach gives exponential time complexity which is not very efficient. Let’s try to optimize the above approach. For that purpose, we need to look at the recursion tree formed by the above approach.

Given below is a partial recursion tree formed when the lcs( ) function is called for the given strings S=” abcde” and T= “ acek “ :

In each block, values of i and j are indicated and below them values of S[ i ] and T[ j ] are indicated.

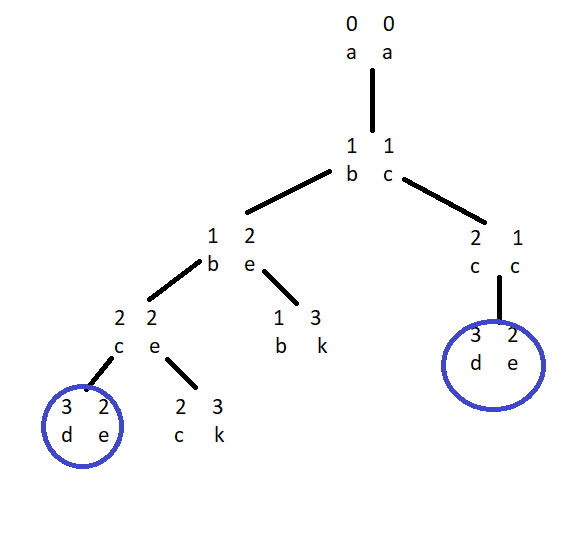We can see that there are some overlapping cases which are recalculated during recursion which is adding to time complexity. We can prevent this recalculation if we remember the overlapping results by storing them somewhere.

Memoization :

When we store the results of the overlapping problems in recursion to speed up the process, it is called memoization.

Let’s make a memo[ ] [ ] table for storing the values. The rows of the table will represent the first string S and the columns will represent the second string T. Initially the table is filled with -1.

The table will look something like this initially.

Now we will utilize the values stored in the table to make our algorithm work faster.

Before making a recursive call for a pair of indices, we will check if the value is already present in the table or not.

If the value is already present in the table, we will consider it, else we will calculate the value and mark it in the table.

Complexity analysis for the above approach :

The number of function calls made depends upon the number of elements stored in the table. This is because a function call is made each time for a pair of indices for which the value in the table is -1. If the value of the pair of indices in the table is not -1, we just look up the stored value and return it.

Number of elements in the table = Length of row * Length of column

                                                    = N * M

Time complexity = O( N * M )
Auxiliary space  = O ( N * M )

We build this table using a top-down approach, as we are solving each problem by solving its subproblem and using the result of the subproblems, further problems are solved.

And using memoization, we reduced the time complexity from $O(2 ^ {(max( N, M)} )$ to $O( N* M)$

Now we will understand the implementation of the above approach.

The optimal substructure for recursive code will remain the same, the only change is that before calling the function for a pair of indices we will look for it in the table, and after calculating the value of each pair we will mark it in the table if not marked already.

Pseudocode :

lcs( S, T , i, j )

    if there are no more characters in either of the strings, return 0.

    else if the value for the current pair is present in the table
         return memo[ i ] [ j ]

else
       {

            if the current characters of both the strings are equal
                 memo[ i ] [ j ] =1 + ( call for the next characters in both the strings )

            else
               memo[ i ][ j ]= maximum of the following 2 calls

1. check the current character of string S with the next character of string T

2. check the current character of string T with the next character of string S

return memo[ i ][ j ]

      }

Implementation:  

• C/C++
• Python

// Recursive implementation of
// Longest Common subsequence problem
// using memoization

#include <bits/stdc++.h>
using namespace std;

const int max_value = 1000;

int N, M;

// For calculating length of longest common subsequence

int lcs(string S, string T, int i, int j, int memo[][max_value])
{
    // one or both of the strings are fully traversed

    if (i == N || j == M)
        return 0;

    // if result for the current pair is already present in
    // the table

    if (memo[i][j] != -1)
        return memo[i][j];

    // check if the current characters in both the strings are equal

    if (S[i] == T[j])
        // check for the next characters in both the strings and store the
        // calculated value in the memo table

        memo[i][j] = lcs(S, T, i + 1, j + 1, memo) + 1;
    else

        // check which call has the maximum value and store in
        // the memo table

        memo[i][j] = max(lcs(S, T, i + 1, j, memo), lcs(S, T, i, j + 1, memo));
    return memo[i][j];
}

// Driver Code

int main()
{
    string S = " abcde";
    string T = "acek";

    N = S.length();
    M = T.length();

    // table for memoization

    int memo[N][max_value];

    // initializing memo table with -1

    for (int i = 0; i < N; i++)
        for (int j = 0; j < M; j++)
            memo[i][j] = -1;

    cout << "Length of longest common subsequence " << lcs(S, T, 0, 0, memo);

    return 0;
}

# Recursive implementation of
# Longest Common subsequence problem
# using memoization

# For calculating length of longest common subsequence


N = 0
M = 0


def lcs(S, T, i, j, memo):

    # one or both of the strings are fully traversed

    if i == N or j == M:
        return 0

    # if result for the current pair is already present in
    # the table

    if memo[i][j] != -1:
        return memo[i][j]

    # check if the current characters in both the strings are equal

    if S[i] == T[j]:

        # check for the next characters in both the strings and store the
        # calculated value in the memo table

        memo[i][j] = lcs(S, T, i + 1, j + 1, memo) + 1
    else:

        # check which call has the maximum value and store in
        # the memo table

        memo[i][j] = max(lcs(S, T, i, j + 1, memo), lcs(S, T, i + 1, j, memo))

    return memo[i][j]


# Driver Code

S = "abcde"
T = "acek"

N = len(S)
M = len(T)


# initializing memo table with -1

memo = [[-1 for i in range(N + 1)] for i in range(M + 1)]

print("Length of longest common subsequence", lcs(S, T, int(0), int(0), memo))