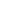Sieve of Eratosthenes is used to get all prime number in a given range and is a very efficient algorithm. You can check more about sieve of Eratosthenes on Wikipedia. It follows the following steps to get all the prime numbers from up to n:
- Make an array of all numbers from 2 to n.
[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ……., n] - Starting from 2, delete all of its multiples in the array, except itself.
[2, 3,4, 5,6, 7,8, 9,10, 11,12, 13,14, 15,16, 17,18, 19,20,……., n] - Repeat the step 2 till square root of n.
For 3 – [2, 3,4, 5,6, 7,8,9,10, 11,12, 13,14,15,16, 17,18, 19,20……., n]
For 5 – [2, 3,4, 5,6, 7,8,9,10, 11,12, 13,14,15,16, 17,18, 19,20……., n]
Till sqrt(n)
The remaining array only contains prime numbers.
Example of first 100 prime numbers
- Step1: Initialize the array – [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100]
- Step2 and step3:
For 2 – [2, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99]
For 3 – [2, 3, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35, 37, 41, 43, 47, 49, 53, 55, 59, 61, 65, 67, 71, 73, 77, 79, 83, 85, 89, 91, 95, 97]
For 4 – (Not in array, deleted during deletion of multiples of 2)
For 5 – [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 49, 53, 59, 61, 67, 71, 73, 77, 79, 83, 89, 91, 97]
For 6 – (Not in array, deleted during deletion of multiples of 2)
For 7 – [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
For 8 – (Not in array, deleted during deletion of multiples of 2)
For 9 – (Not in array, deleted during deletion of multiples of 3)
For 10 [last] (Square root of 100 is 10) – (Not in array, deleted during deletion of multiples of 2) - Final array – [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
C Code for Sieve algorithm
#include <stdio.h>
int main()
{
int number,i,j;
printf("Enter the number\n");
scanf("%d",&number);
int primes[number+1];
//populating array with naturals numbers
for(i = 2; i<=number; i++)
primes[i] = i;
i = 2;
while ((i*i) <= number)
{
if (primes[i] != 0)
{
for(j=2; j<number; j++)
{
if (primes[i]*j > number)
break;
else
// Instead of deleteing , making elemnets 0
primes[primes[i]*j]=0;
}
}
i++;
}
for(i = 2; i<=number; i++)
{
//If number is not 0 then it is prime
if (primes[i]!=0)
printf("%d\n",primes[i]);
}
return 0;
}
for(i = 2; i<=number; i++) primes[i] = i – We are just populating the array with natural numbers.
while ((i*i) <= number) – We will go up till square root of the number.
primes[primes[i]*j]=0 – Making the multiples of the number ‘i’ 0.
Reference – https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes