In Quicksort, we first choose a pivot and then put all the elements smaller than the pivot on one side and all the elements larger than the pivot on another side and then recursively do the same on the smaller subarrays and thus finally sorting the array. Since we are dividing the array and then implementing Quicksort on the smaller arrays, the Quicksort is also a divide and conquer algorithm.
Since everything in this algorithm depends upon the selection of pivot, thus selecting a pivot is the most important part of this algorithm. Generally, there are 4 major ways of choosing a pivot:
- Picking the first element as the pivot
- Picking the last element of the array as the pivot
- Picking a random element
- Picking median
In this post, I will pick the last element of the array as the pivot. So, let's dive into the concepts of writing the code.
The first part of our code will be to implement the partition function i.e., a function to arrange all the elements greater than the pivot on one side and smaller than the pivot on another side of the pivot.
As mentioned above, we are choosing the last element as the pivot. So, the next step is to iterate over the array and put the smaller elements (smaller than pivot) on one side and larger on another. Thus, during the iteration, if the number is larger, we will do nothing but if the element is smaller, then we will just swap it with the larger number. This is described in the picture given below.
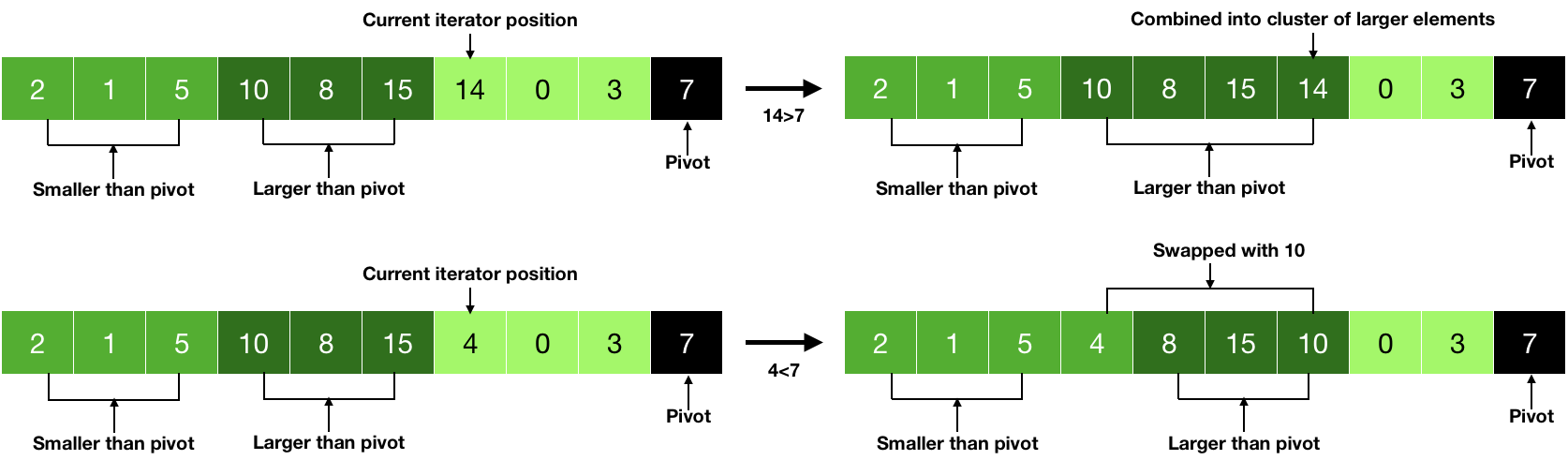

Now, it is clear that we are accumulating the larger and the smaller numbers. In the last step, we will just bring the pivot in the middle i.e., swap the pivot with one of the larger numbers.

After the partition, it is a guarantee that the elements on the right side are smaller than the pivot and the numbers on the left side are larger than the pivot. Now, we can implement the same technique on the smaller subarrays i.e., using the divide part of the divide and conquer and this will finally result in the sorted array.
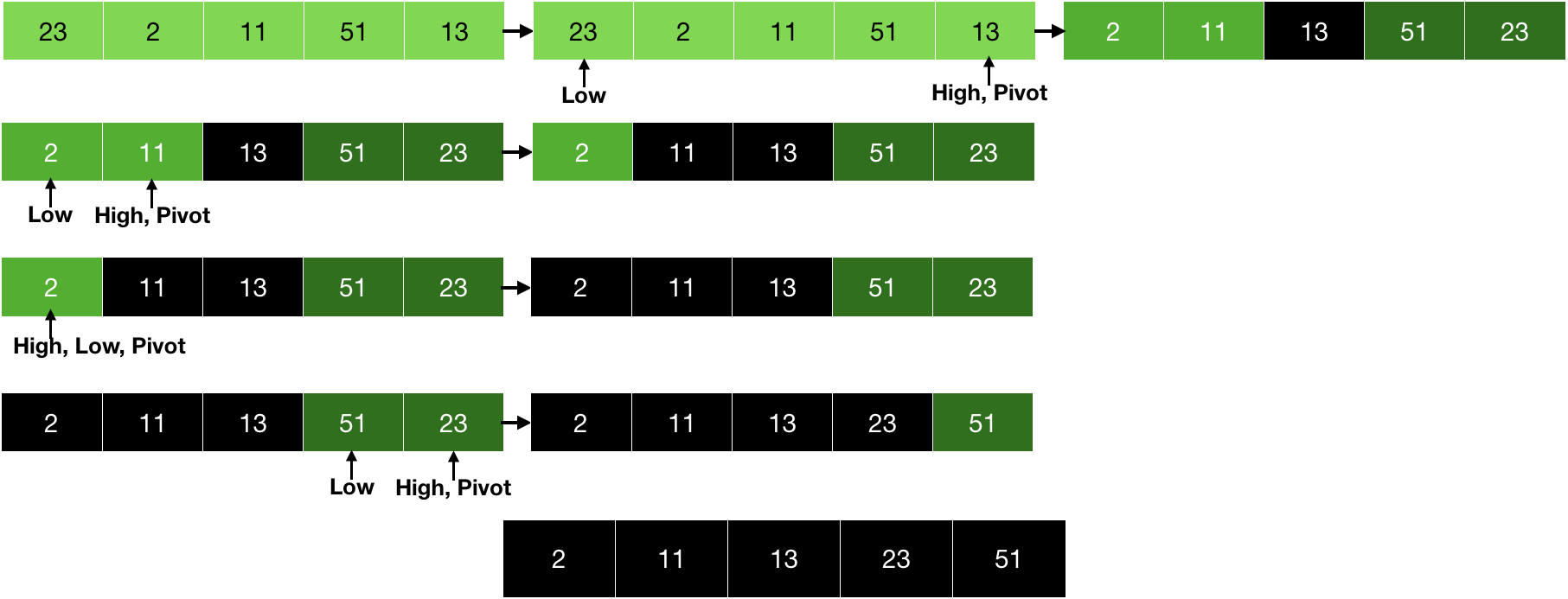
Now, let's write the partition function.
partition(ar, low, high)
// making pivot the last element
pivot = ar[high]
i = low-1
//putting all element smalller than pivot on one side
for j in low to high-1
// element is smaller than pivot
if (ar[j]<=pivot)
// swap the element to put
// all element smaller than
// pivot on one side
i=i+1
swap -> a[i],a[j]
// Lastly, swapping the pivot in the midddle of
// the elements smaller and larger than the pivot
swap -> a[i+1],a[high]
return i+1
pivot = ar[high] - Making the last element pivot.
for j in range(low, high) - Iterating over the array.
if (ar[j]<=pivot) - Number is smaller than the pivot, so we will swap it with the larger number.
i=i+1 - We are keeping the track of the last element of the cluster of the smaller numbers with i and i+1 will give the first element of the cluster of the larger numbers.
swap → a[i],a[j] - Lastly, swapping the pivot with the larger number.
Now, we will write the quicksort function to divide the array and implement partition function on them.
quicksort(ar, low, high)
if (low<high) //array can be further divide into subarrays
// Calling partition function to seperate smaller elements than pivot
// one one side and greater on the another
q = partition(ar, low, high)
// dividing the function into subarrays
quicksort(ar, low, q-1)
quicksort(ar, q+1, high)
if (low<high) - We can further break the array.
q = partition(ar, low, high) - Firstly, partitioning the array and then in the next line, we are implementing the same thing to the subarrays. Here, q is the index of the pivot element returned from the partition function.
Since choosing the pivot is an important part of Quicksort, so the performance of the algorithm also depends heavily on the pivot. If the pivot we are choosing is the middle element i.e., it is a balanced partition, then this is the best case and if the pivot is the smallest or the largest element in every iteration, then it is the worst case.
Like Quicksort, Merge Sort also uses divide and conquer but extra memory is required in the case of Merge Sort to store the array during the runtime but this is not the case with the Quicksort.
C
#include <stdio.h>
// function to swap two integers
void swap( int *a, int *b )
{
int t;
t = *a;
*a = *b;
*b = t;
}
// partition function
int partition(int ar[], int low, int high)
{
// making pivot the last element
int pivot = ar[high];
int i = low-1;
int j;
// putting all element smalller than pivot on one side
for (j=low; j<=high-1; j++)
{
// element is smaller than pivot
if(ar[j]<=pivot)
{
// swap the element to put
// all element smaller than
// pivot on one side
i=i+1;
swap(&ar[i], &ar[j]);
}
}
/*
Lastly, swapping the pivot in the midddle of
the elements smaller and larger than the pivot
*/
swap(&ar[i+1], &ar[high]);
return i+1;
}
/*
Quicksort function. It will call the partition function
to seperate the smaller and greater element than pivot on
two sides. Then it will implement the same thing on smaller arrays
(subarrays) and thus implemens divide and conquer
*/
void quicksort(int ar[], int low, int high)
{
if(low<high) // array can be further divide into subarrays
{
/*
Calling partition function to seperate smaller elements than pivot
one one side and greater on the another
*/
int q = partition(ar, low, high);
// dividing the function into subarrays
quicksort(ar, low, q-1);
quicksort(ar, q+1, high);
}
}
int main()
{
int i;
// array to be sorted
int a[] = {23, 2, 11, 51 ,13};
// calling the quicksort function
quicksort(a, 0, 4);
// printing the array
for (i=0; i<5; i++)
{
printf("%d ",a[i]);
}
// printing new line
printf("\n");
return 0;
}
Python
# partition function
def partition(ar, low, high):
# making pivot the last element
pivot = ar[high]
i = low-1
# putting all element smalller than pivot on one side
for j in range(low, high):
# element is smaller than pivot
if (ar[j]<=pivot):
# swap the element to put
# all element smaller than
# pivot on one side
i=i+1
ar[i], ar[j] = ar[j], ar[i]
'''
Lastly, swapping the pivot in the midddle of
the elements smaller and larger than the pivot
'''
ar[i+1], ar[high] = ar[high], ar[i+1]
return i+1
'''
Quicksort function. It will call the partition function
to seperate the smaller and greater element than pivot on
two sides. Then it will implement the same thing on smaller arrays
(subarrays) and thus implemens divide and conquer
'''
def quicksort(ar, low, high):
if (low<high): #array can be further divide into subarrays
'''
Calling partition function to seperate smaller elements than pivot
one one side and greater on the another
'''
q = partition(ar, low, high)
# dividing the function into subarrays
quicksort(ar, low, q-1)
quicksort(ar, q+1, high)
a = [23, 2, 11, 51 ,13]
quicksort(a, 0, 4)
print(a)
Java
class QuickSort {
static int partition(int ar[], int low, int high)
{
// making pivot the last element
int pivot = ar[high];
int i = low-1;
// putting all element smalller than pivot on one side
for (int j=low; j<=high-1; j++)
{
// element is smaller than pivot
if(ar[j]<=pivot)
{
// swap the element to put
// all element smaller than
// pivot on one side
i=i+1;
int temp;
//swapping
temp = ar[i];
ar[i] = ar[j];
ar[j] = temp;
}
}
/*
Lastly, swapping the pivot in the midddle of
the elements smaller and larger than the pivot
*/
int temp;
temp = ar[i+1];
ar[i+1] = ar[high];
ar[high] = temp;
return i+1;
}
/*
Quicksort function. It will call the partition function
to seperate the smaller and greater element than pivot on
two sides. Then it will implement the same thing on smaller arrays
(subarrays) and thus implemens divide and conquer
*/
static void quicksort(int ar[], int low, int high)
{
if(low<high) // array can be further divide into subarrays
{
/*
Calling partition function to seperate smaller elements than pivot
one one side and greater on the another
*/
int q = partition(ar, low, high);
// dividing the function into subarrays
quicksort(ar, low, q-1);
quicksort(ar, q+1, high);
}
}
public static void main (String[] args) {
int i;
// array to be sorted
int a[] = {23, 2, 11, 51 ,13};
// calling the quicksort function
quicksort(a, 0, 4);
// printing the array
for (i=0; i<5; i++)
{
System.out.print(a[i]+" ");
}
// printing new line
System.out.println("");
}
}







