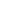Before jumping to Strassen's algorithm, it is necessary that you should be familiar with matrix multiplication using the Divide and Conquer method.
Divide and Conquer Method
Consider two matrices A and B with 4x4 dimension each as shown below,
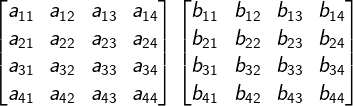
The matrix multiplication of the above two matrices A and B is Matrix C,

where,
$c_{11} = a_{11}*b_{11} + a_{12}*b_{21}+a_{13}*b_{31}+a_{14}*b_{41} \qquad(1)$
$c_{12} = a_{11}*b_{12} + a_{12}*b_{22}+a_{13}*b_{32}+a_{14}*b_{42} \qquad(2)$
$c_{21} = a_{21}*b_{11} + a_{22}*b_{21}+a_{23}*b_{31}+a_{24}*b_{41} \qquad(3)$
$c_{22} = a_{21}*b_{12} + a_{22}*b_{22}+a_{23}*b_{32}+a_{24}*b_{42} \qquad(4)$
and so on.
Now, let's look at the Divide and Conquer approach to multiply two matrices.
Take two submatrices from the above two matrices A and B each as ($A_{11}$ & $A_{12}$) and ($B_{11}$ & $B_{21}$) as shown below,
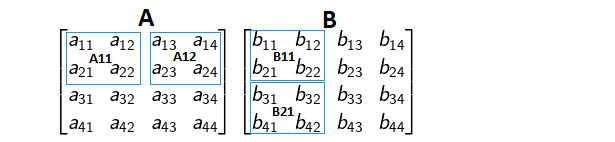
And the matrix multiplication of the two 2x2 matrices A11 and B11 is,

Also, the matrix multiplication of two 2x2 matrices A12 and B21 is as follows,
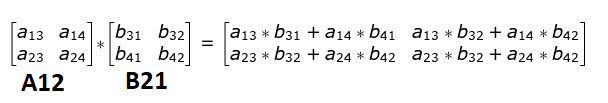
So if you observe, I can conclude the following,
$A_{11}*B_{11} + A_{12}*B_{21} = \begin{bmatrix}
c_{11} & c_{12} & . & . \\
c_{21} & c_{22} & . & . \\
. & . & . & . \\
. & . & . & . \\
\end{bmatrix}$
Where ‘+’ is Matrix Addition,
And $c_{11}$, $c_{12}$, $c_{21}$ and $c_{22}$ are equal to equations 1, 2, 3 and 4 respectively.
So the idea is to recursively divide n x n matrices into n/2 x n/2 matrices until they are small enough to be multiplied in the naive way, more specifically into 8 multiplications and 4 matrix additions as shown below in the code.
Note: Here the dimension n is of the power of 2. You can find a tip somewhere at the end of the article on how to generalize this algorithm for any value of n.
public static int[][] multiply(int[][] A, int[][] B, int rowA, int colA,
int rowB, int colB, int size) {
int[][] C = new int[size][size];
if (size == 1) {
C[0][0] = A[rowA][colA] * B[rowB][colB];
} else {
int newSize = size / 2;
// C11 = A11 * B11 + A12 * B21
add(C, multiply(A, B, rowA, colA, rowB, colB, newSize),//A11*B11
multiply(A, B, rowA, colA + newSize, rowB + newSize, colB, newSize), //A12*B21
0, 0);//C11
// C12 = A11 * B12 + A12 * B22
add(C, multiply(A, B, rowA, colA, rowB, colB + newSize, newSize),//A11*B12
multiply(A, B, rowA, colA + newSize, rowB + newSize, colB + newSize, newSize),//A12*B22
0, newSize);//C12
// C21 = A21 * B11 + A22 * B21
add(C, multiply(A, B, rowA + newSize, colA, rowB, colB, newSize),//A21*B11
multiply(A, B, rowA + newSize, colA + newSize, rowB + newSize, colB, newSize),//A22*B21
newSize,
0);//C21
// C22 = A21 * B12 + A22 * B22
add(C, multiply(A, B, rowA + newSize, colA, rowB, colB + newSize, newSize),//A21*B12
multiply(A, B, rowA + newSize, colA + newSize, rowB + newSize, colB + newSize, newSize), //A22*B22
newSize, newSize);//C22
}
return C;
}
private static void add(int[][] C, int[][] A, int[][] B, int rowC, int colC) {
int n = A.length;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
C[i + rowC][j + colC] = A[i][j] + B[i][j];
}
}
}
}
Recurrence Relation of Divide and Conquer Method
For multiplying two matrices of size n x n, we make 8 recursive calls above, each on a matrix/subproblem with size n/2 x n/2. Each of these recursive calls multiplies two n/2 x n/2 matrices, which are then added together. For addition, we add two matrices of size
$\frac{n^2}{4}$, so each addition takes $\Theta(\frac{n^{2}}{4})$ time. We can write this recurrence in the form of the following equations,
$$T(n) =
\begin{cases}
\Theta(1), & \text{if $n=1$ } \\[2ex]
8T(\frac{n}{2}) + \Theta(n^2), & \text{if $n>1$}
\end{cases}$$
From the Case 1 of Master's Theorem, the time complexity of the above approach is $O(n^{\log_28})$ or $O(n^{3})$ which is the same as the naive method of matrix multiplication.
The Advantage of using Divide and Conquer over the naive method is that we can parallelize the multiplication over different cores and/or cpu’s as the 8 multiplications can be carried out independently.
Strassen’s Algorithm
Strassen’s algorithm makes use of the same divide and conquer approach as above, but instead uses only 7 recursive calls rather than 8 as shown in the equations below. Here we save one recursive call, but have several new additions of n/2 x n/2 matrices.
$M_{1} = (A_{11} + A_{22})(B_{11} + B_{22})$
$M_{2} = (A_{21} + A_{22}) B_{11}$
$M_{3} = A_{11} (B_{12} - B_{22})$
$M_{4} = A_{22} (B_{21} - B-{11})$
$M_{5} = (A_{11} + A_{12}) B_{22}$
$M_{6} = (A_{21} - A_{11}) (B_{11} + B_{12})$
$M_{7} = (A_{12} - A_{22}) (B_{21} + B_{22})$
$C_{11} = M_{1} + M_{4} - M_{5} + M_{7}$
$C_{12} = M_{3} + M_{5}$
$C_{21} = M_{2} + M_{4}$
$C_{22} = M_1 - M_2 + M_3 + M_6$
The above approach is implemented in the following code,
import java.util.Scanner;
/** Class Strassen **/
public class Strassen {
/** Function to multiply matrices **/
public int[][] multiply(int[][] A, int[][] B) {
int n = A.length;
int[][] R = new int[n][n];
/** base case **/
if (n == 1)
R[0][0] = A[0][0] * B[0][0];
else {
int[][] A11 = new int[n / 2][n / 2];
int[][] A12 = new int[n / 2][n / 2];
int[][] A21 = new int[n / 2][n / 2];
int[][] A22 = new int[n / 2][n / 2];
int[][] B11 = new int[n / 2][n / 2];
int[][] B12 = new int[n / 2][n / 2];
int[][] B21 = new int[n / 2][n / 2];
int[][] B22 = new int[n / 2][n / 2];
/** Dividing matrix A into 4 halves **/
split(A, A11, 0, 0);
split(A, A12, 0, n / 2);
split(A, A21, n / 2, 0);
split(A, A22, n / 2, n / 2);
/** Dividing matrix B into 4 halves **/
split(B, B11, 0, 0);
split(B, B12, 0, n / 2);
split(B, B21, n / 2, 0);
split(B, B22, n / 2, n / 2);
/**
* M1 = (A11 + A22)(B11 + B22) M2 = (A21 + A22) B11 M3 = A11 (B12 - B22) M4 =
* A22 (B21 - B11) M5 = (A11 + A12) B22 M6 = (A21 - A11) (B11 + B12) M7 = (A12 -
* A22) (B21 + B22)
**/
int[][] M1 = multiply(add(A11, A22), add(B11, B22));
int[][] M2 = multiply(add(A21, A22), B11);
int[][] M3 = multiply(A11, sub(B12, B22));
int[][] M4 = multiply(A22, sub(B21, B11));
int[][] M5 = multiply(add(A11, A12), B22);
int[][] M6 = multiply(sub(A21, A11), add(B11, B12));
int[][] M7 = multiply(sub(A12, A22), add(B21, B22));
/**
* C11 = M1 + M4 - M5 + M7 C12 = M3 + M5 C21 = M2 + M4 C22 = M1 - M2 + M3 + M6
**/
int[][] C11 = add(sub(add(M1, M4), M5), M7);
int[][] C12 = add(M3, M5);
int[][] C21 = add(M2, M4);
int[][] C22 = add(sub(add(M1, M3), M2), M6);
/** join 4 halves into one result matrix **/
join(C11, R, 0, 0);
join(C12, R, 0, n / 2);
join(C21, R, n / 2, 0);
join(C22, R, n / 2, n / 2);
}
/** return result **/
return R;
}
/** Function to sub two matrices **/
public int[][] sub(int[][] A, int[][] B) {
int n = A.length;
int[][] C = new int[n][n];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
C[i][j] = A[i][j] - B[i][j];
return C;
}
/** Function to add two matrices **/
public int[][] add(int[][] A, int[][] B) {
int n = A.length;
int[][] C = new int[n][n];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
C[i][j] = A[i][j] + B[i][j];
return C;
}
/** Function to split parent matrix into child matrices **/
public void split(int[][] P, int[][] C, int iB, int jB) {
for (int i1 = 0, i2 = iB; i1 < C.length; i1++, i2++)
for (int j1 = 0, j2 = jB; j1 < C.length; j1++, j2++)
C[i1][j1] = P[i2][j2];
}
/** Function to join child matrices into parent matrix **/
public void join(int[][] C, int[][] P, int iB, int jB)
{
for(int i1 = 0, i2 = iB; i1 < C.length; i1++, i2++)
for(int j1 = 0, j2 = jB; j1 < C.length; j1++, j2++)
P[i2][j2] = C[i1][j1];
}
Source: https://www.sanfoundry.com/java-program-strassen-algorithm/
Tip: we can append zeros to the matrices if n is not of the power of 2.
From the above equations, the recurrence relation of the Strassen’s approach is,
$$T(n) =
\begin{cases}
\Theta(1), & \text{if $n=1$ } \\[2ex]
7T(\frac{n}{2}) + \Theta(n^2), & \text{if $n>1$}
\end{cases}$$
So, from Case 1 of Master's Theorem, the time complexity of the above approach is $O(n^{\log_27})$ or $O(n^{2.81})$ which beats the divide and conquer approach asymptotically.
However, $O(n^{2.81})$ is not much improvement though but enough for $n$ having large value as depicted in the graph below,
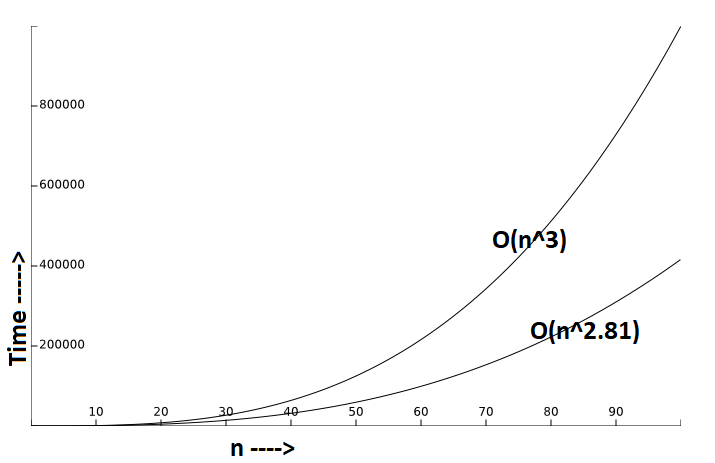
Note: The above graph shows time complexity considering the big $O $notation, actual time may vary based on the implementation and the system used.