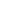Master's method is a quite useful method for solving recurrence equations because it directly gives us the cost of an algorithm with the help of the type of a recurrence equation and it is applied when the recurrence equation is in the form of: $$ T(n) = aT\left(\frac{n}{b}\right) + f(n) $$ where, $a \ge 1$, $b \gt 1$ and $f(n) \gt 0$.
For example,
$c + T\left(\frac{n}{2}\right)$ → $a = 1$, $b = 2$ and $f(n) = c$,
$n+2T\left(\frac{n}{2}\right)$ → $a = 2$, $b = 2$ and $f(n) = n$, etc.
So, let's see what Master Theorem is.
Master's Theorem
Taking an equation of the form: $$ T(n) = aT\left(\frac{n}{b}\right) + f(n) $$ where, $a \ge 1$, $b \gt 1$ and $f(n) \gt 0$
The Master's Theorem states:
- CASE 1 - if $f(n) = O(n^{\log_b{a-\epsilon}})$ for some $\epsilon \gt 0$, then $T(n) = \Theta(n^{\log_ba})$
- CASE 2 - if $f(n) = \Theta(n^{\log_b{a}})$, then $T(n) = \Theta(n^{\log_ba}\lg{n})$
- CASE 3 - if $f(n) = \Omega(n^{\log_b{a+\epsilon}})$ for some $\epsilon \gt 0$, and if $af(n/b) \le cf(n)$ for some $c \lt 1$ and all sufficiently large $n$, then $T(n) = \Theta(f(n))$.
By the use of these three cases, we can easily get the solution of a recurrence equation of the form $T(n) = aT\left(\frac{n}{b}\right) + f(n)$.
If you are having any doubts about Master Theorem, don't worry because we are going to use the Master Theorem on a lot of examples, so you are going to get this.
Idea Behind the Master's Method
The idea behind the Master's method is to compare $n^{\lg_ba}$ with the function $f(n)$ and the entire Master's Theorem is based on this comparison. In layman's term, we are basically finding out which among $n^{\lg_ba}$ and $f(n)$ is dominating another.
For simplification, one can understand the above three cases as:
-
Case 1 - If $f(n)$ is dominated by $n^{\log_ba}$, then $T(n) = \Theta(n^{\log_ba})$.
According to case 1, $f(n) = O(n^{\log_b{a-\epsilon}})$, it means that the worst case of $f(n)$ is $n^{\log_b{a-\epsilon}}$, which is less than $n^{\log_ba}$. So, $n^{\lg_ba}$ is going to take more time and thus dominates. - Case 3 - According to case 3, the best case of the $f(n)$ is $n^{\log_b{a-\epsilon}}$. So, the best case of $f(n)$ is greater than $n^{\log_ba}$ and hence $f(n)$ is going to take more time and thus dominates. So, $T(n)$ is $\Theta(f(n))$
- Case 2 - If $f(n)$ is also $\Theta(n^{\log_ba})$, then the time taken is going to be $\Theta(n^{\log_ba}\lg{n})$
Till now, our entire discussion is based on $n^{\log_ba}$, so one obvious question comes in our mind - Why $n^{\log_ba}$? $T(n)$ is made up of $f(n)$ and $T\left(\frac{n}{b}\right)$, then why we are using $n^{\log_ba}$ to compare with $f(n)$?.
Let's see why.
Why $n^{\log_ba}$?
We have, $$ T(n) = aT\left(\frac{n}{b}\right) + f(n) $$ Let's take the term $aT\left(\frac{n}{b}\right)$ and let $T(n)^{'}$ be the time taken by this term,
The term $aT\left(\frac{n}{b}\right)$ means that our problem of size $n$ is being divided into further $a$ subproblems with each of size $\frac{n}{b}$. So, the total time taken for size $n$ i.e., $T(n)^{'} = a \text{ times } T\left(\frac{n}{b}\right)$ and $T\left(\frac{n}{b}\right)$ is the time taken by each subproblem of size $\frac{n}{b}$.
So, the total time $T(n)^{'} = aT\left(\frac{n}{b}\right)$.
Now, let's analyze $T\left(\frac{n}{b}\right)$.
The size of $T\left(\frac{n}{b}\right)$ will be again divided into $a$ more subproblems of size $\frac{n}{b^2}$.
Thus, $T\left(\frac{n}{b}\right) = aT\left(\frac{n}{b^2}\right)$
$=> T(n)^{'} = aT\left(\frac{n}{b}\right) = a^{2}T\left(\frac{n}{b^2}\right)$
Similarly, we can write $$ T(n)^{'} = aT\left(\frac{n}{b}\right) = a^{2}T\left(\frac{n}{b^2}\right) = a^{3}T\left(\frac{n}{b^3}\right) = a^{i}T\left(\frac{n}{b^i}\right) $$
So, we have the expression of total time taken by the term $aT\left(\frac{n}{b}\right)$ i.e., $a^{i}T\left(\frac{n}{b^i}\right)$.
Let's assume that $n = b^k$ (Similar to the assumption we made earlier - $n = 2^k$, where every time the problem was divided into half of its size)
$=>k = \log_bn$
At level $i$, the size of each subproblem has a size of $n/b^i$. At the last level, the size of the subproblem $= 1$.
$=> \frac{n}{b^i} = 1$
$=> n = b^i => \log_bn=i=k$
Therefore, $i=k$, at the last level.
Using this, we can rewrite $T(n)^{'}$ as
$T(n)^{'} = a^iT\left(\frac{n}{b^i}\right) = a^{\log_bn}\left(\frac{b^i}{b^i}\right)$ ($n = b^k = b^i$)
$= a^{\log_bn}(T(1))$
$= \Theta(a^{\log_bn}) = \Theta(n^{\log_ba})$
Thus, we have seen that the first term is taking a time of $\Theta(n^{\log_ba})$ and that's why we are comparing it with $f(n)$.
So, now we know about Master theorem and why do we use $n^{log_ba}$ for the comparison in the Master's theorem. Let's see some examples of each case of Master's theorem to see how do we really use it.
Examples Using Master's Theorem
Example 1
$$T(n) = 2T\left(\frac{n}{2}\right) + n$$
Here, $a = 2$, $b = 2$, $\log_ba = \log_22 = 1$
Now, $n^{\log_ba} = n^{\log_22} = n$
Also, $f(n) = n$
So, $n^{\log_ba} = n = f(n)$
(comparing $n^{\log_ba}$ with $f(n)$)
$=> f(n) = \Theta(n^{\log_ba})$
So, case 2 can be applied and thus $T(n) = \Theta(n^{\lg_ba}\lg{n}) = \Theta(n\lg{n})$.
Example 2
$$T(n) = 2T\left(\frac{n}{2}\right)+n^2$$
Here, $a = 2$, $b = 2$, $\log_22 = 1$
$=> n^{\lg_ba} = n^1 = n$
$Also, f(n) = n^2$
$=> f(n) = \Omega(n^{1+\epsilon})$ ($\epsilon = 1$) (comparing $n^{\log_ba}$ with $f(n)$)
Case 3 can be applied if rest of the conditions of case 3 gets satisfied for $f(n)$.
The condition is $af(n/b) \le cf(n)$ for some $c \lt 1$ and all sufficiently large $n$.
For a sufficiently large n, we have,
$af\left(\frac{n}{b}\right) = 2f\left(\frac{n}{2}\right) = 2\frac{n^2}{4} = \frac{n^2}{2} \le \frac{1}{2}(n^2)$ (for $c = \frac{1}{2}$)
So, the condition is satisfied for $c =\frac{1}{2}$. Thus, $T(n) = \Theta(f(n)) = \Theta(n^2)$
Example 3
$$ T(n) = 2T\left(\frac{n}{2}\right) + \sqrt n $$
Here, $a = 2$ $b = 2$ $\log_22 = 1$
$n^{\log_22} = n$
$f(n) = \sqrt n$
$f(n) = O(n^{1-\epsilon})$ (Case 2)
$T(n) = \Theta(n)$
Example 4
$$ T(n) = 3T\left(\frac{n}{4}\right) + n\lg{n} $$
Here, $a = 3$ $b = 4$ $\log_43 = 0.792$
$f(n) = \Omega(n^{\log_4{3+\epsilon}})$ (Case 3)
$3\left(\frac{n}{4}\right)\lg{\left(\frac{n}{4}\right)} \le \frac{3}{4}n\lg{n} = c*f(n)$, $c = \frac{3}{4}$
So, $T(n) = \Theta(n\lg{n})$
Example 5
$$ T(n) = 2T\left(\frac{n}{2}\right) + n\lg{n} $$
Here, $a = 2$ $b = 2$ $\log_22 = 1$
$n^{\log_22} = n^1$
$f(n) = n\lg{n}$
$f(n)$ must be polynomially larger by a factor of $n^\epsilon$ but it is only larger by a factor of $\lg{n}$. So, Master's theorem can't be applied.
Example 6
$$ T(n) = 2T(\sqrt n)+\lg{n} $$
The equation here is not in the form of $aT\left(\frac{n}{b}\right) + f(n)$, so we can't apply the Master's theorem directly. But we can make a substitution and convert this equation into a form on which the Master's theorem can be applied.
Let $\lg{n} = m => n = 2^m$
Replacing $n$ with $2^m$,
$T(2^m) = 2T(2^{m/2}) + m$
Let $T(2^m) = S(m)$
$$=> S(m) = 2S\left(\frac{m}{2}\right) + m$$
Now, this equation is in the form of $aT\left(\frac{n}{b}\right) + f(n)$ and is the same equation as it was in example 1. So, we know that $S(m) = O(m\lg{m})$
Now, $T(n) = T(2^m) = S(m) = O(m\lg{m})$
Replacing the value of $m$ with $\lg{n}$,
$=>T(n) = O(\lg{n}\lg{(\lg{n})})$
So, we have learned about algorithms, how to measure their efficiency and what terms to use. Thus, we are now ready with the prerequisite to dive much dipper and real algorithms.