AVL Trees : Insertion, Deletion and Analysis

Similar to red-black trees, AVL (Adelson-Velskii and Landis) trees are also binary search trees which are pretty good balanced. AVL trees use different rules to achieve that balance.

AVL trees use balance factor to get a balanced tree. Balance factor of any node is defined as height(left subtree) - height(right subtree).

balance factor and height in AVL tree

For an AVL tree, the absolute value of balance factor for any node can't be greater than 1 i.e., each node must have a balance factor of either -1, 0 or 1.

Instead of calculating heights of nodes, again and again, we store the current heights in each node. Look at the following picture.

node of AVL tree

If there is only one child of a node, then the height of the other child (empty height) is assumed to be -1. It is shown in the picture given below.

height of empty node in AVL tree

We have claimed that if the balance factors of each node are one of -1, 0 or 1, then the tree is balanced and the height of the tree will be $O(\lg{n})$. Let's prove this claim.

Height of an AVL Tree

Let $N(h)$ be the minimum number of nodes in an AVL tree of height $h$. We can say that $N(0) = 1$ and $N(1) = 2$.

Let there be a node with a height $h$ and one of its child has a height of $h-1$, then for an AVL tree, the minimum height of the other child will be $h-2$.

minimum number of nodes in AVL tree

It means that the minimum number of nodes at height $h$ will be the sum of the minimum number of nodes at heights $h-1$ and $h-2$ + 1 (the node itself).

minimum number of nodes in AVL tree

$N(h) = N(h-1) + N(h-2) + 1$

Replacing $h$ with $h-1$,

$N(h-1) = N(h-2) + N(h-3) + 1$

Replacing the value of $N(h-1)$ in the first equation,

$N(h) = N(h-2) + N(h-3) + 1 + N(h-2) + 1$

or, $N(h) = 2N(h-2) + N(h-3) + 2$

We can also say that,

$N(h) \gt 2N(h-2)$

Similary,

$N(h) \gt 4N(h-4)$
$N(h) \gt 8N(h-8)$

We can write,

$N(h) \gt 2^{i}N(h-2i)$

Choosing the value of $i$ such that $h-2i = 1$.

or, $i = \frac{h}{2} - 1$

Putting this value,

$N(h-2i) = N(1) = 1$

Using this value,

$N(h) \gt 2^{\frac{h}{2} - 1}N(1)$

or, $N(h) \gt 2^{\frac{h}{2} - 1}$

Taking log on both sides,

$\lg{N(h)} \gt \lg{2^{\frac{h}{2} - 1}}$

or, $\lg{N(h)} \gt 2^{\frac{h}{2} - 1}$

or, $2\lg{N(h)} \gt h-2$

or, $h \lt 2\lg{N(h) + 2}$

or, $h = O(\lg{N(h)})$

Since $N(h)$ is the minimum number of nodes, $n \geq N(h)$.

Thus, $h = O(\lg{n})$

So we have proved that the height of an AVL tree is $O(\lg{n})$. This means that we can perform basic search tree opertaions in $O(\lg{n})$ time.

Let's learn about the insertion and deletion in an AVL tree.

Insertion in AVL Tree

Inserting a new node can cause the balance factor of some node to become 2 or -2. In that case, we fix the balance factors by use of rotations. Also, only the heights of the nodes on the path from the insertion point to the root can be changed. So, after inserting, we go back up to the root and update heights of the nodes and if we find any node with a balance factor of 2 or -2, we fix it by rotation.

updated height after insertion in AVL tree

fixing unbalance after insertion in AVL tree

Suppose we have caused unbalance to some node after insertion and the node which needs rebalancing is x.

insertion in AVL tree

The parent of a newly inserted node will have either one child or none prior to insertion. In both the cases, insertion of the node won't cause unbalance of its parent.

parent of new node in AVL tree

However, the grandparent of the new node might lose its balance.

There can be 4 cases of insertion:

Outside Cases (require single rotation)
1. Insertion into left subtree of left child of x.
2. Insertion into right subtree of right child of x.
Inside Cases (require double rotation)
1. Insertion into right subtree of left child of x.
2. Insertion into left subtree of right child of x.

4 cases of insertion in AVL tree

Let's look at the rotations performed for the 4 cases.

Case 1: Insertion into left subtree of left child of x

We do right rotation on the node x.

right rotation on unbalanced node

Case 2: Insertion into right subtree of right child of x

We do left rotation on the node x.

left rotation on unbalanced node

Case 3: Insertion into right subtree of left child of x

We first do left rotation on the left child of x and then right rotation on x.

rotation of inside case in AVL tree

Case 4: Insertion into left subtree of right child of x

We first do right rotation on the right child of x and then left rotation on x.

rotation of inside case in AVL tree

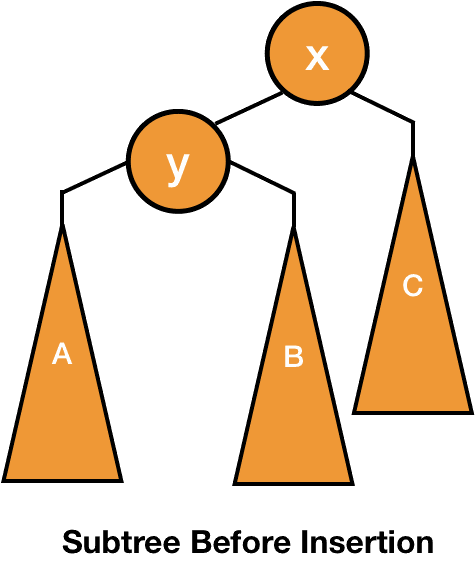
Now, we know what kind of disturbances can occur in the balance of a tree and how to fix them. But we still haven't justified that performing these rotations will fix the balance factor. So, let's look at what happens to the height and the balance factor of the nodes after doing the rotations in inside and outside cases. First, look at the picture of a subtree before insertion.

nodes before insertion in AVL tree

Outside Case

We are going to look at the outside case first and we are assuming that a node is added somewhere in the subtree A and because of it, node x is the first ancestor node which becomes unbalanced.

insertion in subtree of AVL tree

Suppose the height of the root of the node A was initially h and after the insertion, it is h+1. Since root of x is the first node which is unbalance, y is still balanced and initially it was also balanced but its height has been increased because of which x is now unbalanced.

change in height of nodes in AVL tree

Since y is balanced, the root of B can have heights of h, h+1 or h+2. But y was also balanced before insertion, so only possible heights of B are h or h+1. We have also discussed that the height of y increased because of the insertion and this wouldn't have been possible if the height of B was h+1. So, B must have a height of h.

change in height of nodes in AVL tree

Thus, initially the node y had a height of h+1 and now (after insertion), it is h+2. Also, x is now unbalanced but before insertion, it was balanced.

change in height of nodes in AVL tree

The only possible height of C which can make x unbalanced after the insertion is h.

change in height of nodes in AVL tree

Let's perform the right rotation to fix this unbalanced.

rotation to fix unbalance in AVL tree

Before insertion, the root of the subtree (x) has a height of h+2 and now the root of the subtree (y) has also a height of h+2. You can also verify that every node is balanced in the subtree itself. Since the root of the subtree has the same height as before, the unbalance is not going to propagate above it and all the nodes above it will have the same height as before the insertion. So, we have fixed the unbalance.

Let's look at the inside case and see if rotations really work in this case or not.

Inside Case

insertion in inside case in AVL tree

This time, we are assuming that a new node has been added somewhere in the subtree marked in the picture above and because of it, x is the first node which becomes unbalanced. This will happen after an increase in the height of the node y.

unbalanced node in inside case in AVL tree

By the same arguments as stated in the outside case, we can say that the height of A and D must be h.

heights of node in insdie case AVL tree

The node j has a height of h+1 and is balanced, it means that B and C can have heights of either h or h-1. However, one of these must have a height of h because the height of j is h+1.

heights of node in insdie case AVL tree

Let's perform the suitable rotations to fix the unbalance.

rotation to fix unbalance in inside case in AVL tree

Initially, the root of the subtree has a height of h+2 and still it has a height of h+2. So, all the nodes above it must have the same height. You can also check that every node is balanced in the subtree itself. So, we have fixed the unbalance.

Let's look at some examples of insertion:

example of insertion in AVL tree

Code for Insertion

We have already discussed that we are also going to store the height of every node. And these heights can also change during the rotations. So, let's update our previous rotation functions so that they also update the changed heights after rotations.

change in height of node in right rotation

change in height of node in left rotation

As you can see from the above pictures, only the heights of x and y are going to be changed (heights of their ancestors can also change but we will fix them in the insertion process), so will update the heights of x and y only.

x.height = 1 + MAX(HEIGHT(x.left), HEIGHT(x.right))
y.height = 1 + MAX(HEIGHT(y.left), HEIGHT(y.right))

LEFT_ROTATE(T, x)
  y = x.right
  x.right = y.left
  if y.left != NULL
      y.left.parent = x
  y.parent = x.parent
  if x.parent == NULL //x is root
      T.root = y
  elseif x == x.parent.left // x is left child
      x.parent.left = y
  else // x is right child
      x.parent.right = y
  y.left = x
  x.parent = y

  x.height = 1 + MAX(HEIGHT(x.left), HEIGHT(x.right))
  y.height = 1 + MAX(HEIGHT(y.left), HEIGHT(y.right))

We will simply insert the new node (z) as we do in a binary search tree. After that, we will update the heights of its ancestors - node.height = 1 + MAX(HEIGHT(node.left), HEIGHT(node.right)).

i = z.parent
while i != NULL
i.height = 1 + MAX(i.left.height, i.right.height)
i = i.parent

After that, we set x and y as z's grandparent and parent respectively.

if x.parent != NULL
  if x.parent.parent != NULL
    x = z.parent.parent
    y = z.parent

Then we will check if x is balanced or not, and if not, then do suitable rotations among the 4 cases.

if BALANCE-FACTOR(x) <= -2 or BALANCE-FACTOR(x) >= 2 //grandparent is unbalanced
  if y == x.left
    if z == x.left.left //case 1
      RIGHT_ROTATE(T, x)
    else if z == x.left.right //case 3
      LEFT_ROTATION(T, y)
      RIGHT_ROTATE(T, x)
  else if y == x.right
    if z == x.right.right //case 2
      LEFT_ROTATE(T, y)
    else if z == x.right.left //case 4
      RIGHT_ROTATE(T, y)
      LEFT_ROTATE(T, x)

INSERT(T, n)
  temp = T.root
  y = NULL
  while temp != NULL
      y = temp
      if n.data < temp.data
          temp = temp.left
      else
          temp = temp.right
  n.parent = y
  if y==NULL
      T.root = n
  else if n.data < y.data
      y.left = n
  else
      y.right = n

  z = n
  while y != NULL
      y.height = 1 + MAX(HEIGHT(y.left), HEIGHT(y.right))

      x = y.parent
      if BALANCE-FACTOR(x) <= -2 or BALANCE-FACTOR(x) >= 2 //grandparent is unbalanced
          if y == x.left
              if z == x.left.left //case1
                  RIGHT_ROTATE(T, x)
              else if z == x.left.right //case 3
                  LEFT_ROTATE(T, y)
                  RIGHT_ROTATE(T, x)
          else if y == x.right
              if z == x.right.right //case 2
                  LEFT_ROTATET(T, x)
              else if z == x.right.left //case 4
                  RIGHT_ROTATE(T, y)
                  LEFT_ROTATE(T, x)

          break
      y = y.parent
      z = z.parent

We have already updated the heights of ancestors before insertions and also updated heights during rotations. We have also shown that the height of the root of the subtree in which insertion is made is not going to change, so there is no need to re-update the heights of ancestors after rotations.

Deletion in AVL Tree

In deletion also, we delete the node to be deleted in the same way as we do with a normal binary search tree. After that, we fix the unbalance of any ancestor node with suitable rotations. The only thing is that unlike insertion, it might be possible that the unbalance propagates above the tree in deletion which makes us rebalance the ancestor nodes. Let's look at some examples of deletion and then the reason for the same will be clear.

As we have already discussed, there can be three cases of deletion - the node to be deleted has no child, the node to be deleted has one child or the node to be deleted has 2 children. In the third case when the node has 2 children, we replace the content of the nodes with its successor and it reduces to the deletion of the node with either one child or none.

After the deletion procedure, the heights of ancestor nodes will decrease and this may cause unbalance in the tree. Let's look at the loss of balances that can happen and how to fix them.

Let's assume that the first ancestor which is unbalanced is x and y is its child with greater height among the heights of the two children of x. And z is the child of y with greater height among the children of y.

inside and outside case in deletion in AVL tree

We fix the unbalancing by performing the required rotations involving the nodes x, y and z as we did in the insertion part.

Let's talk about the outside case first in which the node x is unbalanced because of the deletion of a node from the subtree a.

outside case of deletion in AVL tree

The height of the subtree a is h before deletion and the node x is balanaced. Since x is balanced, it means that the height of the node y can be h, h-1 or h+1. But after deletion, the height of the subtree a is changed to h-1 and the node x is unbalanced now. It means that the only possible height of the node y can be h+1.

Since z is the child of y with larger height, so its height will be h. As y is balanced, the height of b will be either h or h-1.

The heights of the nodes c and d can be either h-1 or h-2. However, one of these must have a height of h-1 because the height of node x is h.

After deletion, the height of the node a changed to h-1 and thus caused the unbalance on the node x. To fix this, we have performed a right rotation on the node x as we did in insertion.

outside case of deletion in AVL tree

Now, the node y is the root of the subtree. Initially, this subtree has a height of h+2 but now it has a height of h+1 or h+2. If it is changed to h+1, it might have caused unbalance somewhere in its ancestor. In this way, the unbalance propagates above the tree in deletion.

Let's take deletion of inside case.

inside case of deletion in AVL tree

Let's perform the rotations to fix this.

rotaion to fix violation in inside case in deletion in AVL tree

Node z is now the root of the subtree with a height of h+1 which initially was h+2, so we need to check further if any ancestor requires any balancing or not.

One thing should be noted that the subtree d can have a height of either h-1 or h. But if it is h (equal to its sibling), then both children of y have same heights and there isn't a taller child. In that case, we will pick the root of the subtree d as z which will lead to the outside case and thus requiring only one rotation to fix the unbalance. However, the reason for picking the root of the subtree d as z and going for the outside case is not to fix the unbalance in a single rotation only but if we would have picked the other node and gone for the double rotation (inside case), then it wouldn't fix the unbalance. This is shown in the following picture.

inside case when children have same height

Code for Deletion

The code for the deletion is pretty much similar to that of binary search tree. So, let's focus on the rebalancing part.

Similar to the fixing of insertion, we will start with a loop but we will not stop just after fixing an unbalanced node because we have already discussed that the unbalance might propagate above in case of deletion.

AVL_DELETE_FIXUP(T, n)
  p = n

  while p != NULL
      p.height = 1 + MAX(HEIGHT(p.left), HEIGHT(p.right))

      if(BALANCE_FACTOR(p) <= -2 || balance_factor(p) >= 2) //grandparent is unbalanced
          x = p

          //taller child of x will be y
          if x.left.height > x.right.height
              y = x.left
          else
              y = x.right

          //taller child of y will be z
          if y.left.height > y.right.height
              z = y.left
          else if y.left.height < y.right.height
              z = y.right
          else //same height go for single rotation
              if y == x.left
                  z = y.left
              else
                  z = y.right

          //perform rotaions
          if y == x.left
              if z == x.left.left //case1
                  RIGHT_ROTATE(T, x)
              else if z == x.left.right //case 3
                  LEFT_ROTATE(T, y)
                  RIGHT_ROTATE(T, x)
          else if y == x.right
              if z == x.right.right //case 2
                  LEFT_ROTATET(T, x)
              else if z == x.right.left //case 4
                  RIGHT_ROTATE(T, y)
                  LEFT_ROTATE(T, x)
      p = p.parent

Firstly, we have set y as the taller child of x - if x.left.height > x.right.height → ... else → .... Similarly, we have set z as the taller child of y but if the heights of both the children of y are same, we would choose z such that we would have to go for a single rotation - if y == x.left → z = y.left else → z = y.right.

After this, we have just performed the rotation as we did with the insertion part.

DELETE(T, z)
  if z.left == NULL
      TRANSPLANT(T, z, z.right)

      if z.right != NULL
          AVL_DELETE_FIXUP(T, z.right)

  elseif z.right == NULL
      TRANSPLANT(T, z, z.left)

      if z.left != NULL
          AVL_DELETE_FIXUP(T, z.left)

  else
      y = MINIMUM(z.right) //minimum element in right subtree
      if y.parent != z //z is not direct child
          TRANSPLANT(T, y, y.right)
          y.right = z.right
          y.right.parent = y
      TRANSPLANT(T, z, y)
      y.left = z.left
      y.left.parent = y

      if y != NULL
          AVL_DELETE_FIXUP(T, y)

C
Python
Java

#include <stdio.h>
#include <stdlib.h>

typedef struct avl_node {
int data;
struct avl_node *left;
struct avl_node *right;
struct avl_node *parent;
int height;
}avl_node;

typedef struct avl_tree {
avl_node *root;
}avl_tree;

avl_node* new_avl_node(int data) {
avl_node *n = malloc(sizeof(avl_node));
n->data = data;
n->left = NULL;
n->right = NULL;
n->parent = NULL;
n->height = 0;

return n;
}

avl_tree* new_avl_tree() {
avl_tree *t = malloc(sizeof(avl_tree));
t->root = NULL;

return t;
}

int max(int a, int b) {
if(a > b)
  return a;
return b;
}

int height(avl_node *n) {
if(n == NULL)
  return -1;
return n->height;
}

avl_node* minimum(avl_tree *t, avl_node *x) {
while(x->left != NULL)
  x = x->left;
return x;
}

void left_rotate(avl_tree *t, avl_node *x) {
avl_node *y = x->right;
x->right = y->left;
if(y->left != NULL) {
  y->left->parent = x;
}
y->parent = x->parent;
if(x->parent == NULL) { //x is root
  t->root = y;
}
else if(x == x->parent->left) { //x is left child
  x->parent->left = y;
}
else { //x is right child
  x->parent->right = y;
}
y->left = x;
x->parent = y;

x->height = 1 + max(height(x->left), height(x->right));
y->height = 1 + max(height(y->left), height(y->right));
}

void right_rotate(avl_tree *t, avl_node *x) {
avl_node *y = x->left;
x->left = y->right;
if(y->right != NULL) {
  y->right->parent = x;
}
y->parent = x->parent;
if(x->parent == NULL) { //x is root
  t->root = y;
}
else if(x == x->parent->right) { //x is left child
  x->parent->right = y;
}
else { //x is right child
  x->parent->left = y;
}
y->right = x;
x->parent = y;

x->height = 1 + max(height(x->left), height(x->right));
y->height = 1 + max(height(y->left), height(y->right));
}

int balance_factor(avl_node *n) {
if(n == NULL)
  return 0;
return(height(n->left) - height(n->right));
}

void insert(avl_tree *t, avl_node *n) {
avl_node *y = NULL;
avl_node *temp = t->root;
while(temp != NULL) {
  y = temp;
  if(n->data < temp->data)
    temp = temp->left;
  else
    temp = temp->right;
}
n->parent = y;

if(y == NULL) //newly added node is root
  t->root = n;
else if(n->data < y->data)
  y->left = n;
else
  y->right = n;

avl_node *z = n;

while(y != NULL) {
  y->height = 1 + max(height(y->left), height(y->right));


  avl_node *x = y->parent;

  if(balance_factor(x) <= -2 || balance_factor(x) >= 2) {//grandparent is unbalanced
    if(y == x->left) {
      if(z == x->left->left) //case 1
        right_rotate(t, x);

      else if(z == x->left->right) {//case 3
        left_rotate(t, y);
        right_rotate(t, x);
      }
    }
    else if(y == x->right) {
      if(z == x->right->right) //case 2
        left_rotate(t, x);

      else if(z == x->right->left) {//case 4
        right_rotate(t, y);
        left_rotate(t, x);
      }
    }
    break;
  }
  y = y->parent;
  z = z->parent;
}
}

void transplant(avl_tree *t, avl_node *u, avl_node *v) {
if(u->parent == NULL) //u is root
  t->root = v;
else if(u == u->parent->left) //u is left child
  u->parent->left = v;
else //u is right child
  u->parent->right = v;

if(v != NULL)
  v->parent = u->parent;
}

void avl_delete_fixup(avl_tree *t, avl_node *n) {
avl_node *p = n;

while(p != NULL) {
  p->height = 1 + max(height(p->left), height(p->right));

  if(balance_factor(p) <= -2 || balance_factor(p) >= 2) { //grandparent is unbalanced
    avl_node *x, *y, *z;
    x = p;

    //taller child of x will be y
    if(x->left->height > x->right->height)
      y = x->left;
    else
      y = x->right;

    //taller child of y will be z
    if(y->left->height > y->right->height) {
      z = y->left;
    }
    else if(y->left->height < y->right->height) {
      z = y->right;
    }
    else { //same height, go for single rotation
      if(y == x->left)
        z = y->left;
      else
        z = y->right;
    }

    if(y == x->left) {
      if(z == x->left->left) //case 1
        right_rotate(t, x);

      else if(z == x->left->right) {//case 3
        left_rotate(t, y);
        right_rotate(t, x);
      }
    }
    else if(y == x->right) {
      if(z == x->right->right) //case 2
        left_rotate(t, x);

      else if(z == x->right->left) {//case 4
        right_rotate(t, y);
        left_rotate(t, x);
      }
    }
  }
  p = p->parent;
}
}

void avl_delete(avl_tree *t, avl_node *z) {
if(z->left == NULL) {
  transplant(t, z, z->right);
  if(z->right != NULL)
    avl_delete_fixup(t, z->right);
  free(z);
}
else if(z->right == NULL) {
  transplant(t, z, z->left);
  if(z->left != NULL)
    avl_delete_fixup(t, z->left);
  free(z);
}
else {
  avl_node *y = minimum(t, z->right); //minimum element in right subtree
  if(y->parent != z) {
    transplant(t, y, y->right);
    y->right = z->right;
    y->right->parent = y;
  }
  transplant(t, z, y);
  y->left = z->left;
  y->left->parent = y;
  if(y != NULL)
    avl_delete_fixup(t, y);
  free(z);
}
}

void inorder(avl_tree *t, avl_node *n) {
if(n != NULL) {
  inorder(t, n->left);
  printf("%d\n", n->data);
  inorder(t, n->right);
}
}

int main() {
avl_tree *t = new_avl_tree();

avl_node *a, *b, *c, *d, *e, *f, *g, *h, *i, *j, *k, *l, *m;

a = new_avl_node(10);
b = new_avl_node(20);
c = new_avl_node(30);
d = new_avl_node(100);
e = new_avl_node(90);
f = new_avl_node(40);
g = new_avl_node(50);
h = new_avl_node(60);
i = new_avl_node(70);
j = new_avl_node(80);
k = new_avl_node(150);
l = new_avl_node(110);
m = new_avl_node(120);

insert(t, a);
insert(t, b);
insert(t, c);
insert(t, d);
insert(t, e);
insert(t, f);
insert(t, g);
insert(t, h);
insert(t, i);
insert(t, j);
insert(t, k);
insert(t, l);
insert(t, m);

avl_delete(t, a);
avl_delete(t, m);

inorder(t, t->root);

return 0;
}

def max(a, b):
if a > b:
  return a
return b

class AvlNode:
def __init__(self, data):
  self.data = data
  self.right = None
  self.left = None
  self.parent = None
  self.height = 0

class AvlTree:
def __init__(self):
  self.root = None

def height(self, n):
  if n==None:
    return -1
  return n.height

def minimum(self, x):
  while x.left != None:
    x = x.left
  return x

def left_rotate(self, x):
  y = x.right
  x.right = y.left
  if y.left != None:
    y.left.parent = x

  y.parent = x.parent
  if x.parent == None: #x is root
    self.root = y

  elif x == x.parent.left: #x is left child
    x.parent.left = y

  else: #x is right child
    x.parent.right = y

  y.left = x
  x.parent = y

  x.height = 1 + max(self.height(x.left), self.height(x.right))
  y.height = 1 + max(self.height(y.left), self.height(y.right))

def right_rotate(self, x):
  y = x.left
  x.left = y.right
  if y.right != None:
    y.right.parent = x

  y.parent = x.parent
  if x.parent == None: #x is root
    self.root = y

  elif x == x.parent.right: #x is right child
    x.parent.right = y

  else: #x is left child
    x.parent.left = y

  y.right = x
  x.parent = y

  x.height = 1 + max(self.height(x.left), self.height(x.right))
  y.height = 1 + max(self.height(y.left), self.height(y.right))

def balance_factor(self, n):
  if n == None:
    return 0
  return self.height(n.left) - self.height(n.right)

def insert(self, n):
  y = None
  temp = self.root
  while temp != None:
    y = temp
    if n.data < temp.data:
      temp = temp.left
    else:
      temp = temp.right

  n.parent = y

  if y == None: #newly added node is root
    self.root = n
  elif n.data < y.data:
    y.left = n
  else:
    y.right = n

  z = n

  while y != None:
    y.height = 1 + max(self.height(y.left), self.height(y.right))


    x = y.parent

    if self.balance_factor(x) <= -2 or self.balance_factor(x) >= 2:#grandparent is unbalanced
      if y == x.left:
        if z == x.left.left: #case 1
          self.right_rotate(x)

        elif z == x.left.right: #case 3
          self.left_rotate(y)
          self.right_rotate(x)


      elif y == x.right:
        if z == x.right.right: #case 2
          self.left_rotate(x)

        elif z == x.right.left: #case 4
          self.right_rotate(y)
          self.left_rotate(x)

      break

    y = y.parent
    z = z.parent

def transplant(self, u, v):
  if u.parent == None:
    self.root = v
  elif u == u.parent.left:
    u.parent.left = v
  else:
    u.parent.right = v

  if v != None:
    v.parent = u.parent

def avl_delete_fixup(self, n):
  p = n

  while p != None:
    p.height = 1 + max(self.height(p.left), self.height(p.right))

    if self.balance_factor(p) <= -2 or self.balance_factor(p) >= 2: #grandparent is unbalanced
      x = p

      #taller child of x will be y
      if x.left.height > x.right.height:
        y = x.left
      else:
        y = x.right

      #taller child of y will be z
      if y.left.height > y.right.height:
        z = y.left

      elif y.left.height < y.right.height:
        z = y.right

      else: #same height, go for single rotation
        if y == x.left:
          z = y.left
        else:
          z = y.right


      if y == x.left:
        if z == x.left.left: #case 1
          self.right_rotate(x)

        elif z == x.left.right: #case 3
          self.left_rotate(y)
          self.right_rotate(x)

      elif y == x.right:
        if z == x.right.right: #case 2
          self.left_rotate(x)

        elif z == x.right.left: #case 4
          self.right_rotate(y)
          self.left_rotate(x)

    p = p.parent

def delete(self, z):
  if z.left == None:
    self.transplant(z, z.right)
    if z.right != None:
      self.avl_delete_fixup(z.right)

  elif z.right == None:
    self.transplant(z, z.left)
    if z.left != None:
      self.avl_delete_fixup(z.left)

  else:
    y = self.minimum(z.right) #minimum element in right subtree
    if y.parent != z:
      self.transplant(y, y.right)
      y.right = z.right
      y.right.parent = y

    self.transplant(z, y)
    y.left = z.left
    y.left.parent = y
    if y != None:
      self.avl_delete_fixup(y)

def inorder(self, n):
  if n != None:
    self.inorder(n.left)
    print(n.data)
    self.inorder(n.right)

if __name__ == '__main__':
t = AvlTree()

a = AvlNode(10)
b = AvlNode(20)
c = AvlNode(30)
d = AvlNode(100)
e = AvlNode(90)
f = AvlNode(40)
g = AvlNode(50)
h = AvlNode(60)
i = AvlNode(70)
j = AvlNode(80)
k = AvlNode(150)
l = AvlNode(110)
m = AvlNode(120)

t.insert(a)
t.insert(b)
t.insert(c)
t.insert(d)
t.insert(e)
t.insert(f)
t.insert(g)
t.insert(h)
t.insert(i)
t.insert(j)
t.insert(k)
t.insert(l)
t.insert(m)

t.delete(a)
t.delete(m)

t.inorder(t.root)

class AvlNode {
public int data;
public AvlNode left;
public AvlNode right;
public AvlNode parent;
public int height;

public AvlNode(int data) {
  this.data = data;
  this.left = null;
  this.right = null;
  this.parent = null;
  this.height = 0;
}
}

class AvlTree {
public AvlNode root;

public AvlTree() {
  this.root = null;
}

public static int max(int a, int b) {
  if(a > b)
    return a;
  return b;
}

public int height(AvlNode n) {
  if(n == null)
    return -1;
  return n.height;
}

public AvlNode minimum(AvlNode x) {
  while(x.left != null)
    x = x.left;
  return x;
}

public void leftRotate(AvlNode x) {
  AvlNode y = x.right;
  x.right = y.left;
  if(y.left != null) {
    y.left.parent = x;
  }
  y.parent = x.parent;
  if(x.parent == null) { //x is root
    this.root = y;
  }
  else if(x == x.parent.left) { //x is left child
    x.parent.left = y;
  }
  else { //x is right child
    x.parent.right = y;
  }
  y.left = x;
  x.parent = y;

  x.height = 1 + max(height(x.left), height(x.right));
  y.height = 1 + max(height(y.left), height(y.right));
}

public void rightRotate(AvlNode x) {
  AvlNode y = x.left;
  x.left = y.right;
  if(y.right != null) {
    y.right.parent = x;
  }
  y.parent = x.parent;
  if(x.parent == null) { //x is root
    this.root = y;
  }
  else if(x == x.parent.right) { //x is left child
    x.parent.right = y;
  }
  else { //x is right child
    x.parent.left = y;
  }
  y.right = x;
  x.parent = y;

  x.height = 1 + max(height(x.left), height(x.right));
  y.height = 1 + max(height(y.left), height(y.right));
}

public int balanceFactor(AvlNode n) {
  if(n == null)
    return 0;
  return(height(n.left) - height(n.right));
}

public void insert(AvlNode n) {
  AvlNode y = null;
  AvlNode temp = this.root;
  while(temp != null) {
    y = temp;
    if(n.data < temp.data)
      temp = temp.left;
    else
      temp = temp.right;
  }
  n.parent = y;

  if(y == null) //newly added node is root
    this.root = n;
  else if(n.data < y.data)
    y.left = n;
  else
    y.right = n;

  AvlNode z = n;

  while(y != null) {
    y.height = 1 + max(height(y.left), height(y.right));


    AvlNode x = y.parent;

    if(balanceFactor(x) <= -2 || balanceFactor(x) >= 2) {//grandparent is unbalanced
      if(y == x.left) {
        if(z == x.left.left) //case 1
          rightRotate(x);

        else if(z == x.left.right) {//case 3
          leftRotate(y);
          rightRotate(x);
        }
      }
      else if(y == x.right) {
        if(z == x.right.right) //case 2
          leftRotate(x);

        else if(z == x.right.left) {//case 4
          rightRotate(y);
          leftRotate(x);
        }
      }
      break;
    }
    y = y.parent;
    z = z.parent;
  }
}

public void transplant(AvlNode u, AvlNode v) {
  if(u.parent == null) //u is root
    this.root = v;
  else if(u == u.parent.left) //u is left child
    u.parent.left = v;
  else //u is right child
    u.parent.right = v;

  if(v != null)
    v.parent = u.parent;
}

public void avlDeleteFixup(AvlNode n) {
  AvlNode p = n;

  while(p != null) {
    p.height = 1 + max(height(p.left), height(p.right));

    if(balanceFactor(p) <= -2 || balanceFactor(p) >= 2) { //grandparent is unbalanced
      AvlNode x, y, z;
      x = p;

      //taller child of x will be y
      if(x.left.height > x.right.height)
        y = x.left;
      else
        y = x.right;

      //taller child of y will be z
      if(y.left.height > y.right.height) {
        z = y.left;
      }
      else if(y.left.height < y.right.height) {
        z = y.right;
      }
      else { //same height, go for single rotation
        if(y == x.left)
          z = y.left;
        else
          z = y.right;
      }

      if(y == x.left) {
        if(z == x.left.left) //case 1
          rightRotate(x);

        else if(z == x.left.right) {//case 3
          leftRotate(y);
          rightRotate(x);
        }
      }
      else if(y == x.right) {
        if(z == x.right.right) //case 2
          leftRotate(x);

        else if(z == x.right.left) {//case 4
          rightRotate(y);
          leftRotate(x);
        }
      }
    }
    p = p.parent;
  }
}

public void delete(AvlNode z) {
  if(z.left == null) {
    transplant(z, z.right);
    if(z.right != null)
      avlDeleteFixup(z.right);
  }
  else if(z.right == null) {
    transplant(z, z.left);
    if(z.left != null)
      avlDeleteFixup(z.left);
  }
  else {
    AvlNode y = minimum(z.right); //minimum element in right subtree
    if(y.parent != z) {
      transplant(y, y.right);
      y.right = z.right;
      y.right.parent = y;
    }
    transplant(z, y);
    y.left = z.left;
    y.left.parent = y;
    if(y != null)
      avlDeleteFixup(y);
  }
}

public void inorder(AvlNode n) {
  if(n != null) {
    inorder(n.left);
    System.out.println(n.data);
    inorder(n.right);
  }
}

public static void main(String[] args) {
  AvlTree t = new AvlTree();

  AvlNode a, b, c, d, e, f, g, h, i, j, k, l, m;
  a = new AvlNode(10);
  b = new AvlNode(20);
  c = new AvlNode(30);
  d = new AvlNode(100);
  e = new AvlNode(90);
  f = new AvlNode(40);
  g = new AvlNode(50);
  h = new AvlNode(60);
  i = new AvlNode(70);
  j = new AvlNode(80);
  k = new AvlNode(150);
  l = new AvlNode(110);
  m = new AvlNode(120);

  t.insert(a);
  t.insert(b);
  t.insert(c);
  t.insert(d);
  t.insert(e);
  t.insert(f);
  t.insert(g);
  t.insert(h);
  t.insert(i);
  t.insert(j);
  t.insert(k);
  t.insert(l);
  t.insert(m);

  t.delete(a);
  t.delete(m);

  t.inorder(t.root);
}
}

Analysis of AVL Trees

The insertion of a node is going to take $O(\lg{n})$ time because the tree is balanced. Also, the unbalances in the insertion process get fixed after a fixed number of rotations. So, the entire process is of $O(\lg{n})$ time.

We can delete any node in constant time i.e., $O(1)$ and also fix the unbalance with a fixed number of rotations in $O(1)$ time but since the unbalance might propagate above the tree, the entire deletion process takes $O(\lg{n})$ time.

I learned very early the difference between knowing the name of something and knowing something

- Richard P. Feynman