Red-Black Trees | Deletion

The deletion process in a red-black tree is also similar to the deletion process of a normal binary search tree. Similar to the insertion process, we will make a separate function to fix any violations of the properties of the red-black tree.

Just go through the DELETE function of binary search trees because we are going to develop the code for deletion on the basis of that only. After that, we will develop the code to fix the violations.

On the basis of the TRANSPLANT function of a normal binary search tree, we can develop the code for the transplant process for red-black trees as:

RB-TRANSPLANT(T, u, v)
  if u.parent == T.NIL // u is root
      T.root = v
  elseif u == u.parent.left //u is left child
      u.parent.left = v
  else // u is right child
      u.parent.right = v
  v.parent = u.parent

As we are using T.NIL instead of NULL, the last line of the code is getting executed without checking if v is NULL or not (different from binary search tree) because even if v is T.NIL, it will have an arbitrary parent and we can make that as u's parent also.

Let's recap the delete procedure of binary search tree.

In the first two cases when z has less than two children, x is taking the position of y/z.

In the next two cases, y is the minimum of the right subtree of z and x is again taking y's position. We are also replacing the node z with y but we are recoloring it to the original color of z.

Any violations of properties of red-black can only happen because of x taking the position of y. So, we will store the original color of y along the process and use it to see if any property is violated during the process or not.

For x taking the position of y:

• Property 1 can't be violated.
• Property 2 can be violated if y is root and x taking its position is red. In this case, the original color of y will be black.
• Property 3 is not going to be violated.
• Property 4 can be violated only if the parent and child (x) of y are red. In this case also, the original color of y will be black and after removing it, there will be two consecutive reds.
• Property 5 can also be violated only if y is black because removing it will affect the black height of the nodes.

Take a note that any violation is going to happen if the original color of y was black and we will use this as the condition to run the code for fixing the violation.

The above claim can also be justified as if y was red:

• removing it is not going to affect the black height
• if it was red, then it can't be the root, so root is still black
• no red nodes are made consecutive

Let's transform the above picture of deletion in code and then write the code to fix the violation of properties.

Code for Deletion

The deletion code is similar to that of the deletion of a normal binary search tree. You can take a look at that before moving forward for better understanding.

As stated above, we are going to store the original color of y in our process. Initially, we will mark z as y and if we deal with the case where the node z has two children, we will change the node y.

RB-DELETE(T, z)
  y = z
  y_orignal_color = y.color

After this, we will handle the case when the node z has only one child similar to what we did in the delete procedure of a normal binary search tree.

RB-DELETE(T, z)
  ...
  if z.left == T.NIL //no children or only right
    x = z.right
    RB-TRANSPLANT(T, z, z.right)
  else if z.right == T.NIL // only left child
    x = z.left
    RB-TRANSPLANT(T, z, z.left)

The above code is already explained in the binary search tree chapter.

If the node z has both children, then we will mark the smallest element in the z's right subtree as y.

RB-DELETE(T, z)
  ...
  if z.left == T.NIL //no children or only right
    ...
  else if z.right == T.NIL // only left child
    ..
  else // both children
    y = MINIMUM(z.right)
    y_orignal_color = y.color
    x = y.right

The minimum element of the right subtree of z can either be a direct child (right child) of z or it can be a left child of some other node.

We have marked x as the right child of y - x = y.right but it might also be possible that x is T.NIL. In that case, the parent of x will be pointing to any arbitary node and not y. But we need to know the exact parent of x to run the code for fixup. So, we will take caution of pointing the parent of x to y - x.parent = y.

If y is the direct child of z, we will make y as the parent of x right away. In the other case, it will be done further in the process.

RB-DELETE(T, z)
  ...
  if z.left == T.NIL //no children or only right
    ...
  else if z.right == T.NIL // only left child
    ..
  else // both children
    ...
    if y.parent == z // y is direct child of z
      x.parent = y

If y is not the direct child of z, we will first transplant the rigth subtree of y to y - RB-TRANSPLANT(T, y, y.right).

After this, we will change the right of y to right of z -
y.right = z.right
y.right.parent = y

After this we can transplant y to z in both cases (whether y is direct child or not).

RB-DELETE(T, z)
  ...
    ...
    if y.parent == z // y is direct child of z
      x.parent = y
    else
      RB-TRANSPLANT(T, y, y.right)
      y.right = z.right
      y.right.parent = y
    RB-TRANSPLANT(T, z, y)

Next, we will put the left of z to left of y and color y as z.

RB-DELETE(T, z)
  ...
    ...
    if y.parent == z // y is direct child of z
      x.parent = y
    else
      ...
    RB-TRANSPLANT(T, z, y)
    y.left = z.left
    y.left.parent = y
    y.color = z.color

At last, we will call the function to fix the violation if the orignal color of y was black (as discussed above).

RB-DELETE(T, z)
  ...
  if y_orignal_color == black
    RB-DELETE-FIXUP(T, x)

RB-DELETE(T, z)
  y = z
  y_orignal_color = y.color
  if z.left == T.NIL //no children or only right
      x = z.right
      RB-TRANSPLANT(T, z, z.right)
  else if z.right == T.NIL // only left child
      x = z.left
      RB-TRANSPLANT(T, z, z.left)
  else // both children
      y = MINIMUM(z.right)
      y_orignal_color = y.color
      x = y.right
      if y.parent == z // y is direct child of z
          x.parent = y
      else
          RB-TRANSPLANT(T, y, y.right)
          y.right = z.right
          y.right.parent = y
      RB-TRANSPLANT(T, z, y)
      y.left = z.left
      y.left.parent = y
      y.color = z.color
  if y_orignal_color == black
      RB-DELETE-FIXUP(T, x)

Fixing Violation of Red-Black Tree in Deletion

The violation of the property 5 (change in black height) is our main concern. We are going to deal it with a bit different way. We are going to say that the property 5 has not been violated and the node x which is now occupying y's original position has an "extra black" in it. In this way, the property of black height is not violated but the property 1 i.e., every node should be either black or red is violated because the node x is now either "double black" (if it was black) or red and black (if it was red).

With this thinking, we can say that either property 1, 2 or 4 can be violated.

If x is red and black, we can simply color it black and this will fix the violation of the property 1 without causing any other violation. This will also solve the violation of the property 4.

If x is the root, we can simply remove the one extra black and thus, fixing the violation of the property 1.

With the above two mentioned cases, violations of properties 2 and 4 are completely solved and now we can focus only on solving the violation of property 1.

There can be 4 cases (w is x's sibling):

• w is red.
• w is black and its both children are black.
• w is black and its right child is black and left child is red.
• w is black and its right child is red.

For the first case, we can switch the colors of w and its parent and then left rotate the parent of x. In this way, we will enter either case 2, 3 or 4.

For the second case, we will take out one black from both x and w. This will leave x black (it was double black) and y red. For the compensation, we will put one extra black on the parent of x and mark it as the new x and repeat the entire process of fixing the violations for the new x.

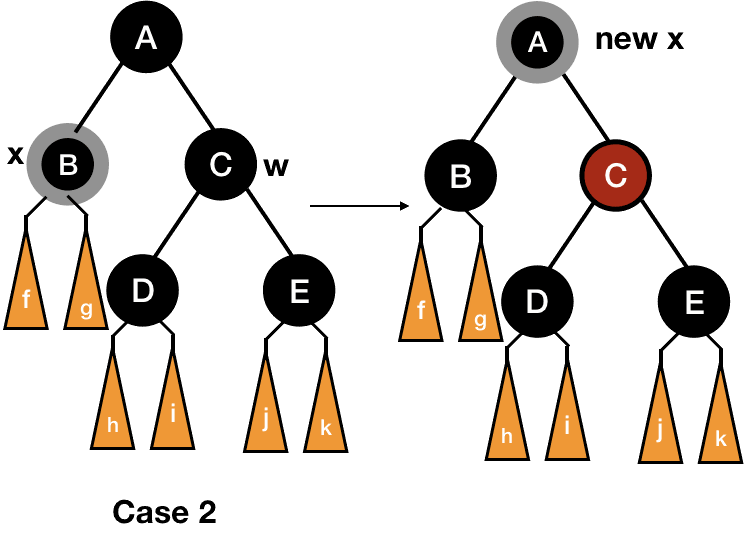
Take note that by doing this, we haven't caused any new violation.

Also if we have entered case 2 from case 1, the parent must be red and now red and black, so it will be simply fixed by coloring it black.

We will transform case 3 to case 4 by switching the colors of w and its left child and then rotating right w.

For case 4, take a look at the following picture:

We first colored w same as the parent of x and then colored the parent of x black. After this, we colored the right child of w black and then left rotated the parent of x. At last, we removed extra black from x without violating any properties.

By now, you must be clear with the way of fixing properties. Let's write the code to do so.

Code of Fixup

Let's look at the code first.

RB-DELETE-FIXUP(T, x)
  while x!= T.root and x.color == black
      if x == x.parent.left
          w = x.parent.right
          if w.color == red //case 1
              w.color = black
              x.parent.color = red
              LEFT-ROTATE(T, x.parent)
              w = x.parent.right
          if w.left.color == black and w.right.color == black //case 2
              w.color = red
              x = x.parent
          else //case 3 or 4
              if w.right.color == black //case 3
                  w.left.color = black
                  w.color = red
                  RIGHT-ROTATE(T, w)
                  w = x.parent.right
              //case 4
              w.color = x.parent.color
              x.parent.color = black
              w.right.color = black
              LEFT-ROTATE(T, x.parent)
              x = T.root
      else
          code will be symmetric
  x.color = black

As we have already discussed, if x is the root or red and black, we will simply color it black. So, the loop can only be executed in those conditions, otherwise, we are doing x.color = black at the last of the code.

The above code is for x being the left child, the code when x is the right child will be symmetric.

Firstly, we have marked the sibling of x as w - w = x.parent.right.

In all the cases, we have just performed all the steps mentioned above.

In the second case, marking the parent of x as x (x = x.parent) will make the while loop iterate on this new x in this iteration.

In the fourth case, we have moved x to the root of the tree - x = T.root because we have already discussed that all the violations will be fixed in this case and we need to terminate the loop. So, making the root of the tree as x will terminate the loop.

• C
• Python
• Java

#include <stdio.h>
#include <stdlib.h>

enum COLOR {Red, Black};

typedef struct tree_node {
int data;
struct tree_node *right;
struct tree_node *left;
struct tree_node *parent;
enum COLOR color;
}tree_node;

typedef struct red_black_tree {
tree_node *root;
tree_node *NIL;
}red_black_tree;

tree_node* new_tree_node(int data) {
tree_node* n = malloc(sizeof(tree_node));
n->left = NULL;
n->right = NULL;
n->parent = NULL;
n->data = data;
n->color = Red;

return n;
}

red_black_tree* new_red_black_tree() {
red_black_tree *t = malloc(sizeof(red_black_tree));
tree_node *nil_node = malloc(sizeof(tree_node));
nil_node->left = NULL;
nil_node->right = NULL;
nil_node->parent = NULL;
nil_node->color = Black;
nil_node->data = 0;
t->NIL = nil_node;
t->root = t->NIL;

return t;
}

void left_rotate(red_black_tree *t, tree_node *x) {
tree_node *y = x->right;
x->right = y->left;
if(y->left != t->NIL) {
  y->left->parent = x;
}
y->parent = x->parent;
if(x->parent == t->NIL) { //x is root
  t->root = y;
}
else if(x == x->parent->left) { //x is left child
  x->parent->left = y;
}
else { //x is right child
  x->parent->right = y;
}
y->left = x;
x->parent = y;
}

void right_rotate(red_black_tree *t, tree_node *x) {
tree_node *y = x->left;
x->left = y->right;
if(y->right != t->NIL) {
  y->right->parent = x;
}
y->parent = x->parent;
if(x->parent == t->NIL) { //x is root
  t->root = y;
}
else if(x == x->parent->right) { //x is left child
  x->parent->right = y;
}
else { //x is right child
  x->parent->left = y;
}
y->right = x;
x->parent = y;
}

void insertion_fixup(red_black_tree *t, tree_node *z) {
while(z->parent->color == Red) {
  if(z->parent == z->parent->parent->left) { //z.parent is the left child

    tree_node *y = z->parent->parent->right; //uncle of z

    if(y->color == Red) { //case 1
      z->parent->color = Black;
      y->color = Black;
      z->parent->parent->color = Red;
      z = z->parent->parent;
    }
    else { //case2 or case3
      if(z == z->parent->right) { //case2
        z = z->parent; //marked z.parent as new z
        left_rotate(t, z);
      }
      //case3
      z->parent->color = Black; //made parent black
      z->parent->parent->color = Red; //made parent red
      right_rotate(t, z->parent->parent);
    }
  }
  else { //z.parent is the right child
    tree_node *y = z->parent->parent->left; //uncle of z

    if(y->color == Red) {
      z->parent->color = Black;
      y->color = Black;
      z->parent->parent->color = Red;
      z = z->parent->parent;
    }
    else {
      if(z == z->parent->left) {
        z = z->parent; //marked z.parent as new z
        right_rotate(t, z);
      }
      z->parent->color = Black; //made parent black
      z->parent->parent->color = Red; //made parent red
      left_rotate(t, z->parent->parent);
    }
  }
}
t->root->color = Black;
}

void insert(red_black_tree *t, tree_node *z) {
tree_node* y = t->NIL; //variable for the parent of the added node
tree_node* temp = t->root;

while(temp != t->NIL) {
  y = temp;
  if(z->data < temp->data)
    temp = temp->left;
  else
    temp = temp->right;
}
z->parent = y;

if(y == t->NIL) { //newly added node is root
  t->root = z;
}
else if(z->data < y->data) //data of child is less than its parent, left child
  y->left = z;
else
  y->right = z;

z->right = t->NIL;
z->left = t->NIL;

insertion_fixup(t, z);
}

void rb_transplant(red_black_tree *t, tree_node *u, tree_node *v) {
if(u->parent == t->NIL)
  t->root = v;
else if(u == u->parent->left)
  u->parent->left = v;
else
  u->parent->right = v;
v->parent = u->parent;
}

tree_node* minimum(red_black_tree *t, tree_node *x) {
while(x->left != t->NIL)
  x = x->left;
return x;
}

void rb_delete_fixup(red_black_tree *t, tree_node *x) {
while(x != t->root && x->color == Black) {
  if(x == x->parent->left) {
    tree_node *w = x->parent->right;
    if(w->color == Red) {
      w->color = Black;
      x->parent->color = Red;
      left_rotate(t, x->parent);
      w = x->parent->right;
    }
    if(w->left->color == Black && w->right->color == Black) {
      w->color = Red;
      x = x->parent;
    }
    else {
      if(w->right->color == Black) {
        w->left->color = Black;
        w->color = Red;
        right_rotate(t, w);
        w = x->parent->right;
      }
      w->color = x->parent->color;
      x->parent->color = Black;
      w->right->color = Black;
      left_rotate(t, x->parent);
      x = t->root;
    }
  }
  else {
    tree_node *w = x->parent->left;
    if(w->color == Red) {
      w->color = Black;
      x->parent->color = Red;
      right_rotate(t, x->parent);
      w = x->parent->left;
    }
    if(w->right->color == Black && w->left->color == Black) {
      w->color = Red;
      x = x->parent;
    }
    else {
      if(w->left->color == Black) {
        w->right->color = Black;
        w->color = Red;
        left_rotate(t, w);
        w = x->parent->left;
      }
      w->color = x->parent->color;
      x->parent->color = Black;
      w->left->color = Black;
      right_rotate(t, x->parent);
      x = t->root;
    }
  }
}
x->color = Black;
}

void rb_delete(red_black_tree *t, tree_node *z) {
tree_node *y = z;
tree_node *x;
enum COLOR y_orignal_color = y->color;
if(z->left == t->NIL) {
  x = z->right;
  rb_transplant(t, z, z->right);
}
else if(z->right == t->NIL) {
  x = z->left;
  rb_transplant(t, z, z->left);
}
else {
  y = minimum(t, z->right);
  y_orignal_color = y->color;
  x = y->right;
  if(y->parent == z) {
    x->parent = z;
  }
  else {
    rb_transplant(t, y, y->right);
    y->right = z->right;
    y->right->parent = y;
  }
  rb_transplant(t, z, y);
  y->left = z->left;
  y->left->parent = y;
  y->color = z->color;
}
if(y_orignal_color == Black)
  rb_delete_fixup(t, x);
}

void inorder(red_black_tree *t, tree_node *n) {
if(n != t->NIL) {
  inorder(t, n->left);
  printf("%d\n", n->data);
  inorder(t, n->right);
}
}

int main() {
red_black_tree *t = new_red_black_tree();

tree_node *a, *b, *c, *d, *e, *f, *g, *h, *i, *j, *k, *l, *m;
a = new_tree_node(10);
b = new_tree_node(20);
c = new_tree_node(30);
d = new_tree_node(100);
e = new_tree_node(90);
f = new_tree_node(40);
g = new_tree_node(50);
h = new_tree_node(60);
i = new_tree_node(70);
j = new_tree_node(80);
k = new_tree_node(150);
l = new_tree_node(110);
m = new_tree_node(120);

insert(t, a);
insert(t, b);
insert(t, c);
insert(t, d);
insert(t, e);
insert(t, f);
insert(t, g);
insert(t, h);
insert(t, i);
insert(t, j);
insert(t, k);
insert(t, l);
insert(t, m);

rb_delete(t, a);
rb_delete(t, m);

inorder(t, t->root);

return 0;
}

Red = 'Red'
Black = 'Black'

class TreeNode:
def __init__(self, data):
  self.left = None
  self.right = None
  self.parent = None
  self.data = data
  self.color = Red

class RedBlackTree:
def __init__(self):
  nil_node = TreeNode(0)
  nil_node.color = Black
  self.NIL = nil_node
  self.root = self.NIL

def left_rotate(self, x):
  y = x.right
  x.right = y.left
  if y.left != self.NIL:
    y.left.parent = x
  y.parent = x.parent
  if x.parent == self.NIL: #x is root
    self.root = y
  elif x == x.parent.left: #x is left child
    x.parent.left = y
  else: #x is right child
    x.parent.right = y
  y.left = x
  x.parent = y

def right_rotate(self, x):
  y = x.left
  x.left = y.right
  if y.right != self.NIL:
    y.right.parent = x
  y.parent = x.parent
  if x.parent == self.NIL: #x is root
    self.root = y
  elif x == x.parent.right: #x is right child
    x.parent.right = y
  else: #x is left child
    x.parent.left = y
  y.right = x
  x.parent = y

def insert_fixup(self, z):
  while z.parent.color == Red:
    if z.parent == z.parent.parent.left: #z.parent is the left child

      y = z.parent.parent.right #uncle of z

      if y.color == Red: #case 1
        z.parent.color = Black
        y.color = Black
        z.parent.parent.color = Red
        z = z.parent.parent

      else: #case2 or case3
        if z == z.parent.right: #case2
          z = z.parent #marked z.parent as new z
          self.left_rotate(z)

        #case3
        z.parent.color = Black #made parent black
        z.parent.parent.color = Red #made parent red
        self.right_rotate(z.parent.parent)

    else: #z.parent is the right child
      y = z.parent.parent.left #uncle of z

      if y.color == Red:
        z.parent.color = Black
        y.color = Black
        z.parent.parent.color = Red
        z = z.parent.parent

      else:
        if z == z.parent.left:
          z = z.parent #marked z.parent as new z
          self.right_rotate(z)

        z.parent.color = Black #made parent black
        z.parent.parent.color = Red #made parent red
        self.left_rotate(z.parent.parent)

  self.root.color = Black

def insert(self, z):
  y = self.NIL #variable for the parent of the added node
  temp = self.root

  while temp != self.NIL:
    y = temp
    if z.data < temp.data:
      temp = temp.left
    else:
      temp = temp.right

  z.parent = y

  if y == self.NIL: #newly added node is root
    self.root = z

  elif z.data < y.data: #data of child is less than its parent, left child
    y.left = z
  else:
    y.right = z

  z.right = self.NIL
  z.left = self.NIL

  self.insert_fixup(z)

def rb_transplant(self, u, v):
  if u.parent == self.NIL:
    self.root = v
  elif u == u.parent.left:
    u.parent.left = v
  else:
    u.parent.right = v
  v.parent = u.parent

def minimum(self, x):
  while x.left != self.NIL:
    x = x.left
  return x

def delete_fixup(self, x):
  while x != self.root and x.color == Black:
    if x == x.parent.left:
      w = x.parent.right
      if w.color == Red:
        w.color = Black
        x.parent.color = Red
        self.left_rotate(x.parent)
        w = x.parent.right

      if w.left.color == Black and w.right.color == Black:
        w.color = Red
        x = x.parent

      else:
        if w.right.color == Black:
          w.left.color = Black
          w.color = Red
          self.right_rotate(w)
          w = x.parent.right

        w.color = x.parent.color
        x.parent.color = Black
        w.right.color = Black
        self.left_rotate(x.parent)
        x = self.root

    else:
      w = x.parent.left
      if w.color == Red:
        w.color = Black
        x.parent.color = Red
        self.right_rotate(x.parent)
        w = x.parent.left

      if w.right.color == Black and w.left.color == Black:
        w.color = Red
        x = x.parent

      else:
        if w.left.color == Black:
          w.right.color = Black
          w.color = Red
          self.left_rotate(w)
          w = x.parent.left

        w.color = x.parent.color
        x.parent.color = Black
        w.left.color = Black
        self.right_rotate(x.parent)
        x = self.root

  x.color = Black

def rb_delete(self, z):
  y = z
  x = None
  y_orignal_color = y.color
  if z.left == self.NIL:
    x = z.right
    self.rb_transplant(z, z.right)

  elif z.right == self.NIL:
    x = z.left
    self.rb_transplant(z, z.left)

  else:
    y = self.minimum(z.right)
    y_orignal_color = y.color
    x = y.right
    if y.parent == z:
      x.parent = z

    else:
      self.rb_transplant(y, y.right)
      y.right = z.right
      y.right.parent = y

    self.rb_transplant(z, y)
    y.left = z.left
    y.left.parent = y
    y.color = z.color

  if y_orignal_color == Black:
    self.delete_fixup(x)

def inorder(self, n):
  if n != self.NIL:
    self.inorder(n.left)
    print(n.data)
    self.inorder(n.right)

if __name__ == '__main__':
t = RedBlackTree()

a = TreeNode(10)
b = TreeNode(20)
c = TreeNode(30)
d = TreeNode(100)
e = TreeNode(90)
f = TreeNode(40)
g = TreeNode(50)
h = TreeNode(60)
i = TreeNode(70)
j = TreeNode(80)
k = TreeNode(150)
l = TreeNode(110)
m = TreeNode(120)

t.insert(a)
t.insert(b)
t.insert(c)
t.insert(d)
t.insert(e)
t.insert(f)
t.insert(g)
t.insert(h)
t.insert(i)
t.insert(j)
t.insert(k)
t.insert(l)
t.insert(m)

t.rb_delete(a)
t.rb_delete(m)

t.inorder(t.root)

enum Color {
Red, Black
}

class TreeNode {
public int data;
public TreeNode right;
public TreeNode left;
public TreeNode parent;
public Color color;

public TreeNode(int data) {
  this.left = null;
  this.right = null;
  this.parent = null;
  this.data = data;
  this.color = Color.Red;
}
}

class RedBlackTree {
TreeNode root;
TreeNode NIL;

public RedBlackTree() {
  TreeNode nilNode = new TreeNode(0);
  nilNode.color = Color.Black;
  this.NIL = nilNode;
  this.root = this.NIL;
}

public void leftRotate(TreeNode x) {
  TreeNode y = x.right;
  x.right = y.left;
  if(y.left != this.NIL) {
    y.left.parent = x;
  }
  y.parent = x.parent;
  if(x.parent == this.NIL) { //x is root
    this.root = y;
  }
  else if(x == x.parent.left) { //x is left child
    x.parent.left = y;
  }
  else { //x is right child
    x.parent.right = y;
  }
  y.left = x;
  x.parent = y;
}

public void rightRotate(TreeNode x) {
  TreeNode y = x.left;
  x.left = y.right;
  if(y.right != this.NIL) {
    y.right.parent = x;
  }
  y.parent = x.parent;
  if(x.parent == this.NIL) { //x is root
    this.root = y;
  }
  else if(x == x.parent.right) { //x is left child
    x.parent.right = y;
  }
  else { //x is right child
    x.parent.left = y;
  }
  y.right = x;
  x.parent = y;
}

public void insertFixup(TreeNode z) {
  while(z.parent.color == Color.Red) {
    if(z.parent == z.parent.parent.left) { //z.parent is the left child

      TreeNode y = z.parent.parent.right; //uncle of z

      if(y.color == Color.Red) { //case 1
        z.parent.color = Color.Black;
        y.color = Color.Black;
        z.parent.parent.color = Color.Red;
        z = z.parent.parent;
      }
      else { //case2 or case3
        if(z == z.parent.right) { //case2
          z = z.parent; //marked z.parent as new z
          leftRotate(z);
        }
        //case3
        z.parent.color = Color.Black; //made parent black
        z.parent.parent.color = Color.Red; //made parent red
        rightRotate(z.parent.parent);
      }
    }
    else { //z.parent is the right child
      TreeNode y = z.parent.parent.left; //uncle of z

      if(y.color == Color.Red) {
        z.parent.color = Color.Black;
        y.color = Color.Black;
        z.parent.parent.color = Color.Red;
        z = z.parent.parent;
      }
      else {
        if(z == z.parent.left) {
          z = z.parent; //marked z.parent as new z
          rightRotate(z);
        }
        z.parent.color = Color.Black; //made parent black
        z.parent.parent.color = Color.Red; //made parent red
        leftRotate(z.parent.parent);
      }
    }
  }
  this.root.color = Color.Black;
}

public void insert(TreeNode z) {
  TreeNode y = this.NIL; //variable for the parent of the added node
  TreeNode temp = this.root;

  while(temp != this.NIL) {
    y = temp;
    if(z.data < temp.data)
      temp = temp.left;
    else
      temp = temp.right;
  }
  z.parent = y;

  if(y == this.NIL) { //newly added node is root
    this.root = z;
  }
  else if(z.data < y.data) //data of child is less than its parent, left child
    y.left = z;
  else
    y.right = z;

  z.right = this.NIL;
  z.left = this.NIL;

  insertFixup(z);
}

public void rbTransplant(TreeNode u, TreeNode v) {
  if(u.parent == this.NIL)
    this.root = v;
  else if(u == u.parent.left)
    u.parent.left = v;
  else
    u.parent.right = v;
  v.parent = u.parent;
}

public TreeNode minimum(TreeNode x) {
  while(x.left != this.NIL)
    x = x.left;
  return x;
}

public void deleteFixup(TreeNode x) {
  while(x != this.root && x.color == Color.Black) {
    if(x == x.parent.left) {
      TreeNode w = x.parent.right;
      if(w.color == Color.Red) {
        w.color = Color.Black;
        x.parent.color = Color.Red;
        leftRotate(x.parent);
        w = x.parent.right;
      }
      if(w.left.color == Color.Black && w.right.color == Color.Black) {
        w.color = Color.Red;
        x = x.parent;
      }
      else {
        if(w.right.color == Color.Black) {
          w.left.color = Color.Black;
          w.color = Color.Red;
          rightRotate(w);
          w = x.parent.right;
        }
        w.color = x.parent.color;
        x.parent.color = Color.Black;
        w.right.color = Color.Black;
        leftRotate(x.parent);
        x = this.root;
      }
    }
    else {
      TreeNode w = x.parent.left;
      if(w.color == Color.Red) {
        w.color = Color.Black;
        x.parent.color = Color.Red;
        rightRotate(x.parent);
        w = x.parent.left;
      }
      if(w.right.color == Color.Black && w.left.color == Color.Black) {
        w.color = Color.Red;
        x = x.parent;
      }
      else {
        if(w.left.color == Color.Black) {
          w.right.color = Color.Black;
          w.color = Color.Red;
          leftRotate(w);
          w = x.parent.left;
        }
        w.color = x.parent.color;
        x.parent.color = Color.Black;
        w.left.color = Color.Black;
        rightRotate(x.parent);
        x = this.root;
      }
    }
  }
  x.color = Color.Black;
}

public void rbDelete(TreeNode z) {
  TreeNode y = z;
  TreeNode x;
  Color yOrignalColor = y.color;
  if(z.left == this.NIL) {
    x = z.right;
    rbTransplant(z, z.right);
  }
  else if(z.right == this.NIL) {
    x = z.left;
    rbTransplant(z, z.left);
  }
  else {
    y = minimum(z.right);
    yOrignalColor = y.color;
    x = y.right;
    if(y.parent == z) {
      x.parent = z;
    }
    else {
      rbTransplant(y, y.right);
      y.right = z.right;
      y.right.parent = y;
    }
    rbTransplant(z, y);
    y.left = z.left;
    y.left.parent = y;
    y.color = z.color;
  }
  if(yOrignalColor == Color.Black)
    deleteFixup(x);
}

public void inorder(TreeNode n) {
  if(n != this.NIL) {
    inorder(n.left);
    System.out.println(n.data);
    inorder(n.right);
  }
}

public static void main(String[] args) {
  RedBlackTree t = new RedBlackTree();

  TreeNode a, b, c, d, e, f, g, h, i, j, k, l, m;
  a = new TreeNode(10);
  b = new TreeNode(20);
  c = new TreeNode(30);
  d = new TreeNode(100);
  e = new TreeNode(90);
  f = new TreeNode(40);
  g = new TreeNode(50);
  h = new TreeNode(60);
  i = new TreeNode(70);
  j = new TreeNode(80);
  k = new TreeNode(150);
  l = new TreeNode(110);
  m = new TreeNode(120);

  t.insert(a);
  t.insert(b);
  t.insert(c);
  t.insert(d);
  t.insert(e);
  t.insert(f);
  t.insert(g);
  t.insert(h);
  t.insert(i);
  t.insert(j);
  t.insert(k);
  t.insert(l);
  t.insert(m);

  t.rbDelete(a);
  t.rbDelete(m);

  t.inorder(t.root);
}
}

Analysis of Deletion Process

Cases 1, 3 and 4 terminate without any further iteration of the loop. Only case 2 can cause the loop to iterate and in that case, x can move up until the root which can take $O(\lg{n})$ time. So, the entire process can run in $O(\lg{n})$ time.