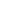Red Black Trees : Rotations and Insertions

Before moving to the procedure of insertion and deletion, let's look at an important operation which is not only used by red-black trees but many other binary search trees also.

Rotations in Binary Search Tree

There are two types of rotations:

Left Rotation
Right Rotation

In left rotation, we assume that the right child is not null. Similarly, in the right rotation, we assume that the left child is not null.

Consider the following tree:

binary search tree

After applying left rotation on the node x, the node y will become the new root of the subtree and its left child will be x. And the previous left child of y will now become the right child of x.

left rotation on binary search tree

animation of left rotation on binary search tree

Now applying right rotation on the node y of the rotated tree, it will transform back to the original tree.

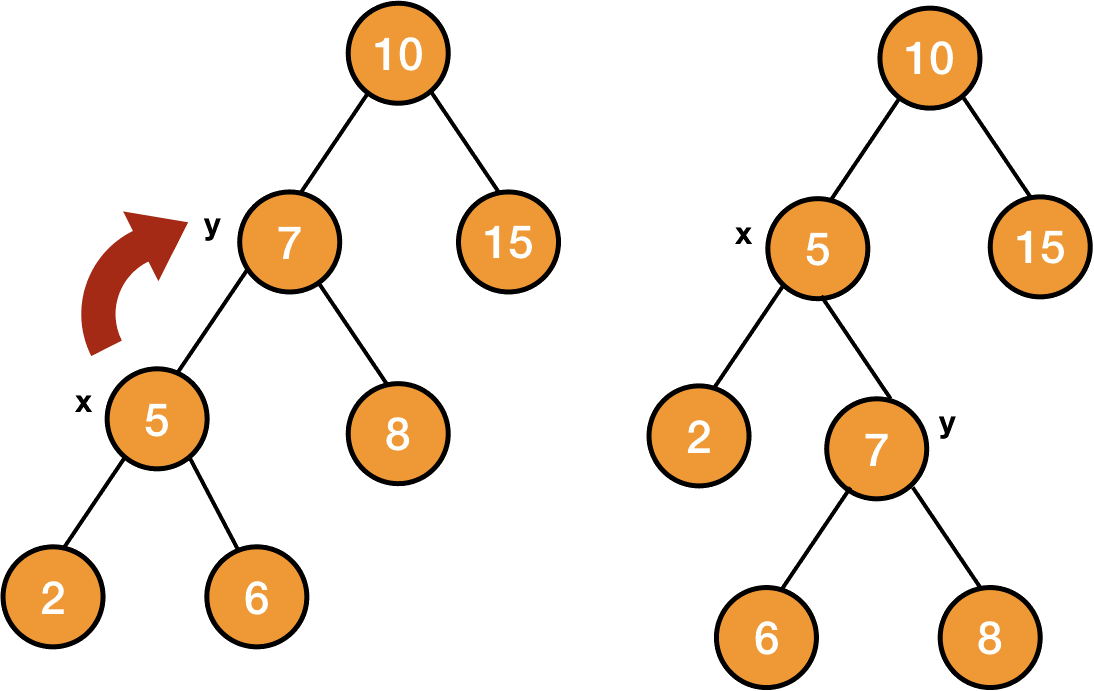
right rotation on binary search tree

So right rotation on the node y will make x the root of the tree, y will become x's right child. And the previous right child of x will now become the left child of y.

animation of right rotation on binary search tree

Take a note that rotation doesn't violate the property of binary search trees.

Code of Rotations

We are going to explain the code for left rotation here. The code for the right rotation will be symmetric.

We need the tree T and the node x on which we are going to apply the rotation - LEFT_ROTATION(T, x).

The left grandchild of x (left child of the right child x) will become the right child of it after rotation. We will do this but before doing this, let's mark the right child of x as y.

code for left rotation on binary search tree

LEFT_ROTATION(T, x)
y = x.right
x.right = y.left

The left child of y is going to be the right child of x - x.right = y.left. We also need to change the parent of y.left to x. We will do this if the left child of y is not NULL.

if y.left != NULL
y.left.parent = x

Then we need to put y to the position of x. We will first change the parent of y to the parent of x - y.parent = x.parent. After this, we will make the node x the child of y's parent instead of y. We will do so by checking if y is the right or left child of its parent. We will also check if y is the root of the tree.

y.parent = x.parent
if x.parent == NULL //x is root
  T.root = y
elseif x == x.parent.left // x is left child
  x.parent.left = y
else // x is right child
  x.parent.right = y

At last, we need to make x the left child of y.

y.left = x
x.parent = y

LEFT_ROTATE(T, x)
  y = x.right
  x.right = y.left
  if y.left != NULL
      y.left.parent = x
  y.parent = x.parent
  if x.parent == NULL //x is root
      T.root = y
  elseif x == x.parent.left // x is left child
      x.parent.left = y
  else // x is right child
      x.parent.right = y
  y.left = x
  x.parent = y

From the above code, you can easily see that rotation is a constant time taking process ($O(1)$).

Now that we know how to perform rotation, we will use this to restore red-black properties when they get violated after adding or deleting any node. So, let's learn to insert a new node to a red-black tree.

Insertion

We insert a new node to a red-black tree in a similar way as we do in a normal binary search tree. We just call a function at the last to fix any kind of violations that could have occurred in the process of insertion.

We color any newly inserted node to red. Doing so can violate the property 4 of red-black trees which we will fix after the insertion process as stated above. There can be a violation of property 2 also but it can be easily fixed by coloring the root black. Also, there can't be any other violations.

new red node in red black tree

So, we will fix these properties after inserting the node.

Since there can't be consecutive red nodes, the changes that this violation could happen is half. Also, fixing the violation of property 4 is easy. Think of a case when the newly inserted node is black. This would affect the black height and fixing that would be difficult. This is the reason why we don't color any new node to black.

Code for Insertion

As told earlier, the entire code for insertion is the same and we will just call a function to fix the violation of properties of red-black trees. We will also color the newly added node to red.

INSERT(T, n)
  y = T.NIL
  temp = T.root

  while temp != T.NIL
      y = temp
      if n.data < temp.data
          temp = temp.left
      else
          temp = temp.right
  n.parent = y
  if y==T.NIL
      T.root = n
  else if n.data < y.data
      y.left = n
  else
      y.right = n

  n.left = T.NIL
  n.right = T.NIL
  n.color = RED
  INSERT_FIXUP(T, n)

Here, we have used T.NIL instead of NULL unlike we do with normal binary search tree. Also, those T.NIL are the leaves and they all are black, so there won't be a violation of property 3.

In the last few lines, we are making the left and right of the new node T.NIL and also making it red. At last, we are calling the function to fix the violations of the red-black properties. Rest of the code is similar to a normal binary search tree.

Let's focus on the function to fix the violations.

The property 4 will be violated when the parent of the inserted node is red. So, we will fix the violations if the parent of the new node is red. At last, we will color the root black and that will fix the violation of property 2 if it is violated. In the case of violation of property 4 (when the parent of the new node is red), the grandparent will be black.

grandparent of new node

There can be six cases in the case of violation of the property 4. Let's look at the given pictures first assuming that the parent of the node z is a left child of its parent which gives us the first three cases. The other three cases will be symmetric when the node z will be the right child of its parent.

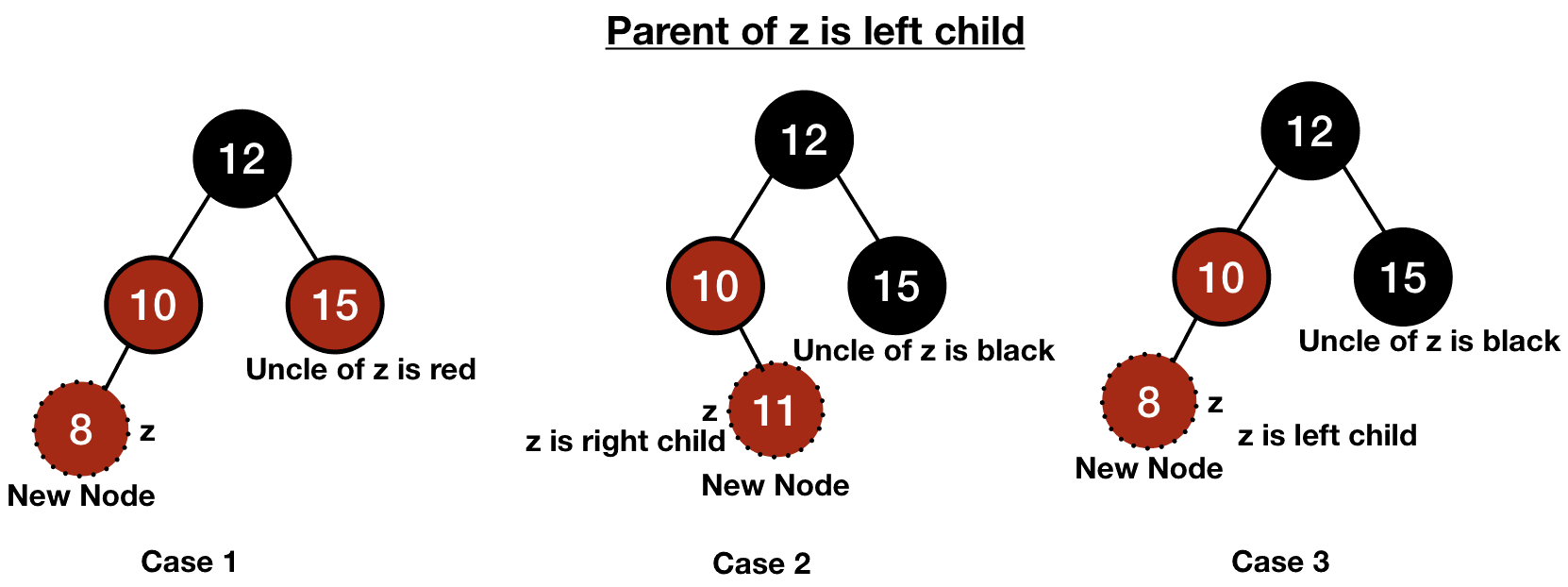
cases of violation of red black property

The first case is when the uncle of z is also red. In this case, we will shift the red color upward until there is no violation. Otherwise, if it reaches to the root, we can just color it black without any consequences.

first case of violation of red black property

So, the process is to make both the parent and the uncle of z black and its grandparent red. In this way, the black height of any node won't be affected and we can successfully shift the red color upward.

However, making the grandparent of z red might cause violation of the property 4 there. So, we will do the fixup again on that node.

first case of violation of red black property

In the second case, the uncle of the node z is black and the node z is the right child.

In the third case, the uncle of the node z is black and the node z is the left child.

We can transform the second case into the third one by performing left rotation on the parent of the node z. Since both z and its parent are red, so rotation won't affect the black height.

second case of violation of red black property

In case 3, we first color the parent of the node z black and its grandparent red and then do a right rotation on the grandparent of the node z. This fixes the violation of properties completely. This is shown in the picture given below.

third case of violation of red black property

Since we are making the parent of z black in both case 2 and case 3, the loop will stop in these two cases.

Let's look at the following example first.

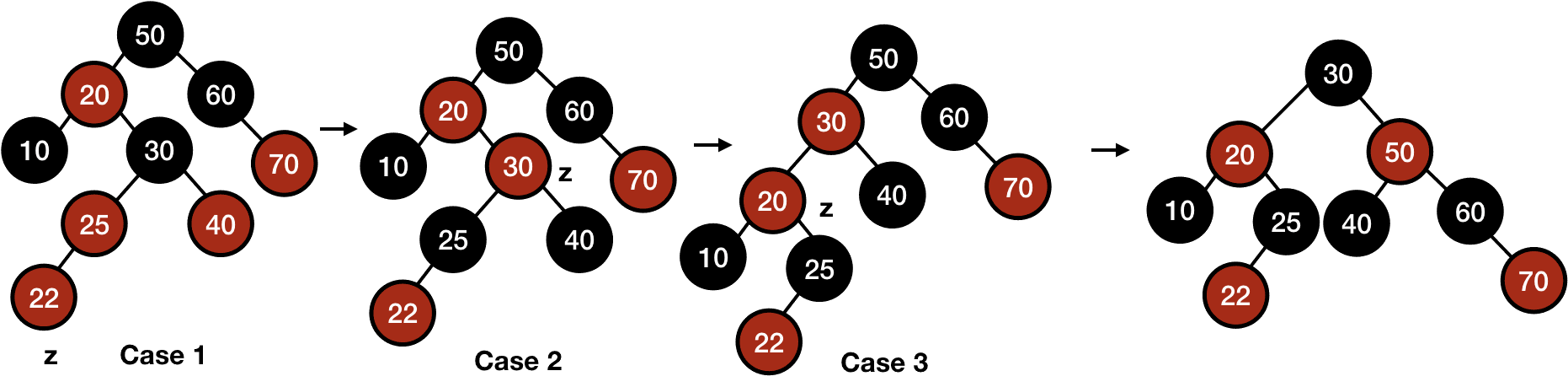
fixing violation of red black property during insertion

Similarly, there will be three cases when the parent of z will be the right child but those cases will be symmetric to the above cases only with left and right exchanged.

Let's implement the above concepts into code.

Code for Fixup

Let's look at the code for fixing the violation first.

INSERT_FIXUP(T, z)
  while z.parent.color == red

      if z.parent == z.parent.parent.left //z.parent is left child
          y = z.parent.parent.right //uncle of z

          if y.color == red //case 1
              z.parent.color = black
              y.color = black
              z.parent.parent.color = red
              z = z.parent.parent

          else //case 2 or 3
              if z == z.parent.right //case 2
                  z = z.parent //marked z.parent as new z
                  LEFT_ROTATE(T, z) //rotated parent of orignal z

              //case 3
              z.parent.color = black // made parent black
              z.parent.parent.color = red // made grandparent red
              RIGHT_ROTATE(T, z.parent.parent) // right rotation on grandparent

      else // z.parent is right child
          code will be symmetric
  T.root.color = black

We need to pass the tree and the node added to the function - INSERT-FIXUP(T, z). As discussed above, in case of the violation of the property 4, the parent of the node will be red, so we need to perform fixup only if the parent of z is red. At last, we will color the root black which will fix the violation of the property 2 if it is violated.

INSERT-FIXUP(T, z)
while z.parent.color == red
...

We are going to write the code when the parent of z is the left child. The code when the parent of z is the right child will be symmetric.

INSERT-FIXUP(T, z)
  while z.parent.color == red
    if z.parent == z.parent.parent.left //z.parent is left child
      ...
    else // z.parent is right child
      code will be symmetric

Next, we have marked the uncle of z as y. Now, the first case is when the color of the node y is red.

In that case, we need to change the color of the parent and the uncle to black and the grandparent to red. After doing this, we shifted z two levels up and now we need to check if the grandparent is violating the rules or not. Therefore, we will point z to its grandparent i.e., z = z.parent.parent. It is shown in the picture given below.

first case of violation of red black property

Since z.parent.parent is new the z, the loop will check it for violations as it is z now.

INSERT-FIXUP(T, z)
  while z.parent.color == red
    if z.parent == z.parent.parent.left //z.parent is left child
      y = z.parent.parent.right //uncle of z

      if y.color == black // case 1
        z.parent.color = black
        y.color = black
        z.parent.parent.color = red
        z = z.parent.parent // loop will check this new z

If y is not red, then we will have either case 2 or case 3. If z is the right child, then it will be case 2.

INSERT-FIXUP(T, z)
  while z.parent.color == red
    if z.parent == z.parent.parent.left //z.parent is left child
      y = z.parent.parent.right //uncle of z

      if y.color == black // case 1
        ...

      else //case 2 or 3
        if z = z.parent.right // case 2

As we have discussed, we are going to transform case 2 to case 3 by doing a left rotation on the parent of z and mark it as new z.

INSERT-FIXUP(T, z)
  while z.parent.color == red
    if z.parent == z.parent.parent.left //z.parent is left child
      y = z.parent.parent.right //uncle of z

      if y.color == black // case 1
        ...

      else //case 2 or 3
        if z = z.parent.right // case 2
          z = z.parent // marked z.parent as new z
          LEFT_ROTATE(T, z) //rotated parent of orignal z

After this, we will handle case 3. We will make the parent of z black and its grandparent red. Then, we will do a right rotation on its grandparent.

third case of violation of red black property

z.parent.color = black
z.parent.parent.color = red
RIGHT_ROTATE(T, z.parent.parent)

Either case 2 or case 3 is making the parent of z black. In both the cases, the loop is not going to iterate further.

At last, we need to make the root of the tree black because it might be possible that case 1 led the red node up till root.

INSERT-FIXUP(T, z)
  while z.parent.color == red
    if z.parent == z.parent.parent.left //z.parent is left child
      ...

      if y.color == black // case 1
        ...

      else
        ...

  T.root.color = black

C
Python
Java

#include <stdio.h>
#include <stdlib.h>

enum COLOR {Red, Black};

typedef struct tree_node {
int data;
struct tree_node *right;
struct tree_node *left;
struct tree_node *parent;
enum COLOR color;
}tree_node;

typedef struct red_black_tree {
tree_node *root;
tree_node *NIL;
}red_black_tree;

tree_node* new_tree_node(int data) {
tree_node* n = malloc(sizeof(tree_node));
n->left = NULL;
n->right = NULL;
n->parent = NULL;
n->data = data;
n->color = Red;

return n;
}

red_black_tree* new_red_black_tree() {
red_black_tree *t = malloc(sizeof(red_black_tree));
tree_node *nil_node = malloc(sizeof(tree_node));
nil_node->left = NULL;
nil_node->right = NULL;
nil_node->parent = NULL;
nil_node->color = Black;
nil_node->data = 0;
t->NIL = nil_node;
t->root = t->NIL;

return t;
}

void left_rotate(red_black_tree *t, tree_node *x) {
tree_node *y = x->right;
x->right = y->left;
if(y->left != t->NIL) {
  y->left->parent = x;
}
y->parent = x->parent;
if(x->parent == t->NIL) { //x is root
  t->root = y;
}
else if(x == x->parent->left) { //x is left child
  x->parent->left = y;
}
else { //x is right child
  x->parent->right = y;
}
y->left = x;
x->parent = y;
}

void right_rotate(red_black_tree *t, tree_node *x) {
tree_node *y = x->left;
x->left = y->right;
if(y->right != t->NIL) {
  y->right->parent = x;
}
y->parent = x->parent;
if(x->parent == t->NIL) { //x is root
  t->root = y;
}
else if(x == x->parent->right) { //x is left child
  x->parent->right = y;
}
else { //x is right child
  x->parent->left = y;
}
y->right = x;
x->parent = y;
}

void insertion_fixup(red_black_tree *t, tree_node *z) {
while(z->parent->color == Red) {
  if(z->parent == z->parent->parent->left) { //z.parent is the left child

    tree_node *y = z->parent->parent->right; //uncle of z

    if(y->color == Red) { //case 1
      z->parent->color = Black;
      y->color = Black;
      z->parent->parent->color = Red;
      z = z->parent->parent;
    }
    else { //case2 or case3
      if(z == z->parent->right) { //case2
        z = z->parent; //marked z.parent as new z
        left_rotate(t, z);
      }
      //case3
      z->parent->color = Black; //made parent black
      z->parent->parent->color = Red; //made parent red
      right_rotate(t, z->parent->parent);
    }
  }
  else { //z.parent is the right child
    tree_node *y = z->parent->parent->left; //uncle of z

    if(y->color == Red) {
      z->parent->color = Black;
      y->color = Black;
      z->parent->parent->color = Red;
      z = z->parent->parent;
    }
    else {
      if(z == z->parent->left) {
        z = z->parent; //marked z.parent as new z
        right_rotate(t, z);
      }
      z->parent->color = Black; //made parent black
      z->parent->parent->color = Red; //made parent red
      left_rotate(t, z->parent->parent);
    }
  }
}
t->root->color = Black;
}

void insert(red_black_tree *t, tree_node *z) {
tree_node* y = t->NIL; //variable for the parent of the added node
tree_node* temp = t->root;

while(temp != t->NIL) {
  y = temp;
  if(z->data < temp->data)
    temp = temp->left;
  else
    temp = temp->right;
}
z->parent = y;

if(y == t->NIL) { //newly added node is root
  t->root = z;
}
else if(z->data < y->data) //data of child is less than its parent, left child
  y->left = z;
else
  y->right = z;

z->right = t->NIL;
z->left = t->NIL;

insertion_fixup(t, z);
}

void inorder(red_black_tree *t, tree_node *n) {
if(n != t->NIL) {
  inorder(t, n->left);
  printf("%d\n", n->data);
  inorder(t, n->right);
}
}

int main() {
red_black_tree *t = new_red_black_tree();

tree_node *a, *b, *c, *d, *e, *f, *g, *h, *i, *j, *k, *l, *m;
a = new_tree_node(10);
b = new_tree_node(20);
c = new_tree_node(30);
d = new_tree_node(100);
e = new_tree_node(90);
f = new_tree_node(40);
g = new_tree_node(50);
h = new_tree_node(60);
i = new_tree_node(70);
j = new_tree_node(80);
k = new_tree_node(150);
l = new_tree_node(110);
m = new_tree_node(120);

insert(t, a);
insert(t, b);
insert(t, c);
insert(t, d);
insert(t, e);
insert(t, f);
insert(t, g);
insert(t, h);
insert(t, i);
insert(t, j);
insert(t, k);
insert(t, l);
insert(t, m);

inorder(t, t->root);

return 0;
}

Red = 'Red'
Black = 'Black'

class TreeNode:
def __init__(self, data):
  self.left = None
  self.right = None
  self.parent = None
  self.data = data
  self.color = Red

class RedBlackTree:
def __init__(self):
  nil_node = TreeNode(0)
  nil_node.color = Black
  self.NIL = nil_node
  self.root = self.NIL

def left_rotate(self, x):
  y = x.right
  x.right = y.left
  if y.left != self.NIL:
    y.left.parent = x
  y.parent = x.parent
  if x.parent == self.NIL: #x is root
    self.root = y
  elif x == x.parent.left: #x is left child
    x.parent.left = y
  else: #x is right child
    x.parent.right = y
  y.left = x
  x.parent = y

def right_rotate(self, x):
  y = x.left
  x.left = y.right
  if y.right != self.NIL:
    y.right.parent = x
  y.parent = x.parent
  if x.parent == self.NIL: #x is root
    self.root = y
  elif x == x.parent.right: #x is right child
    x.parent.right = y
  else: #x is left child
    x.parent.left = y
  y.right = x
  x.parent = y

def insert_fixup(self, z):
  while z.parent.color == Red:
    if z.parent == z.parent.parent.left: #z.parent is the left child

      y = z.parent.parent.right #uncle of z

      if y.color == Red: #case 1
        z.parent.color = Black
        y.color = Black
        z.parent.parent.color = Red
        z = z.parent.parent

      else: #case2 or case3
        if z == z.parent.right: #case2
          z = z.parent #marked z.parent as new z
          self.left_rotate(z)

        #case3
        z.parent.color = Black #made parent black
        z.parent.parent.color = Red #made parent red
        self.right_rotate(z.parent.parent)

    else: #z.parent is the right child
      y = z.parent.parent.left #uncle of z

      if y.color == Red:
        z.parent.color = Black
        y.color = Black
        z.parent.parent.color = Red
        z = z.parent.parent

      else:
        if z == z.parent.left:
          z = z.parent #marked z.parent as new z
          self.right_rotate(z)

        z.parent.color = Black #made parent black
        z.parent.parent.color = Red #made parent red
        self.left_rotate(z.parent.parent)

  self.root.color = Black

def insert(self, z):
  y = self.NIL #variable for the parent of the added node
  temp = self.root

  while temp != self.NIL:
    y = temp
    if z.data < temp.data:
      temp = temp.left
    else:
      temp = temp.right

  z.parent = y

  if y == self.NIL: #newly added node is root
    self.root = z

  elif z.data < y.data: #data of child is less than its parent, left child
    y.left = z
  else:
    y.right = z

  z.right = self.NIL
  z.left = self.NIL

  self.insert_fixup(z)

def inorder(self, n):
  if n != self.NIL:
    self.inorder(n.left)
    print(n.data)
    self.inorder(n.right)

if __name__ == '__main__':
t = RedBlackTree()

a = TreeNode(10)
b = TreeNode(20)
c = TreeNode(30)
d = TreeNode(100)
e = TreeNode(90)
f = TreeNode(40)
g = TreeNode(50)
h = TreeNode(60)
i = TreeNode(70)
j = TreeNode(80)
k = TreeNode(150)
l = TreeNode(110)
m = TreeNode(120)

t.insert(a)
t.insert(b)
t.insert(c)
t.insert(d)
t.insert(e)
t.insert(f)
t.insert(g)
t.insert(h)
t.insert(i)
t.insert(j)
t.insert(k)
t.insert(l)
t.insert(m)

t.inorder(t.root)

enum Color {
Red, Black
}

class TreeNode {
public int data;
public TreeNode right;
public TreeNode left;
public TreeNode parent;
public Color color;

public TreeNode(int data) {
  this.left = null;
  this.right = null;
  this.parent = null;
  this.data = data;
  this.color = Color.Red;
}
}

class RedBlackTree {
TreeNode root;
TreeNode NIL;

public RedBlackTree() {
  TreeNode nilNode = new TreeNode(0);
  nilNode.color = Color.Black;
  this.NIL = nilNode;
  this.root = this.NIL;
}

public void leftRotate(TreeNode x) {
  TreeNode y = x.right;
  x.right = y.left;
  if(y.left != this.NIL) {
    y.left.parent = x;
  }
  y.parent = x.parent;
  if(x.parent == this.NIL) { //x is root
    this.root = y;
  }
  else if(x == x.parent.left) { //x is left child
    x.parent.left = y;
  }
  else { //x is right child
    x.parent.right = y;
  }
  y.left = x;
  x.parent = y;
}

public void rightRotate(TreeNode x) {
  TreeNode y = x.left;
  x.left = y.right;
  if(y.right != this.NIL) {
    y.right.parent = x;
  }
  y.parent = x.parent;
  if(x.parent == this.NIL) { //x is root
    this.root = y;
  }
  else if(x == x.parent.right) { //x is left child
    x.parent.right = y;
  }
  else { //x is right child
    x.parent.left = y;
  }
  y.right = x;
  x.parent = y;
}

public void insertFixup(TreeNode z) {
  while(z.parent.color == Color.Red) {
    if(z.parent == z.parent.parent.left) { //z.parent is the left child

      TreeNode y = z.parent.parent.right; //uncle of z

      if(y.color == Color.Red) { //case 1
        z.parent.color = Color.Black;
        y.color = Color.Black;
        z.parent.parent.color = Color.Red;
        z = z.parent.parent;
      }
      else { //case2 or case3
        if(z == z.parent.right) { //case2
          z = z.parent; //marked z.parent as new z
          leftRotate(z);
        }
        //case3
        z.parent.color = Color.Black; //made parent black
        z.parent.parent.color = Color.Red; //made parent red
        rightRotate(z.parent.parent);
      }
    }
    else { //z.parent is the right child
      TreeNode y = z.parent.parent.left; //uncle of z

      if(y.color == Color.Red) {
        z.parent.color = Color.Black;
        y.color = Color.Black;
        z.parent.parent.color = Color.Red;
        z = z.parent.parent;
      }
      else {
        if(z == z.parent.left) {
          z = z.parent; //marked z.parent as new z
          rightRotate(z);
        }
        z.parent.color = Color.Black; //made parent black
        z.parent.parent.color = Color.Red; //made parent red
        leftRotate(z.parent.parent);
      }
    }
  }
  this.root.color = Color.Black;
}

public void insert(TreeNode z) {
  TreeNode y = this.NIL; //variable for the parent of the added node
  TreeNode temp = this.root;

  while(temp != this.NIL) {
    y = temp;
    if(z.data < temp.data)
      temp = temp.left;
    else
      temp = temp.right;
  }
  z.parent = y;

  if(y == this.NIL) { //newly added node is root
    this.root = z;
  }
  else if(z.data < y.data) //data of child is less than its parent, left child
    y.left = z;
  else
    y.right = z;

  z.right = this.NIL;
  z.left = this.NIL;

  insertFixup(z);
}

public void inorder(TreeNode n) {
  if(n != this.NIL) {
    inorder(n.left);
    System.out.println(n.data);
    inorder(n.right);
  }
}

public static void main(String[] args) {
  RedBlackTree t = new RedBlackTree();

  TreeNode a, b, c, d, e, f, g, h, i, j, k, l, m;
  a = new TreeNode(10);
  b = new TreeNode(20);
  c = new TreeNode(30);
  d = new TreeNode(100);
  e = new TreeNode(90);
  f = new TreeNode(40);
  g = new TreeNode(50);
  h = new TreeNode(60);
  i = new TreeNode(70);
  j = new TreeNode(80);
  k = new TreeNode(150);
  l = new TreeNode(110);
  m = new TreeNode(120);

  t.insert(a);
  t.insert(b);
  t.insert(c);
  t.insert(d);
  t.insert(e);
  t.insert(f);
  t.insert(g);
  t.insert(h);
  t.insert(i);
  t.insert(j);
  t.insert(k);
  t.insert(l);
  t.insert(m);

  t.inorder(t.root);
}
}

Analysis of Insertion

The insertion of a new node will be performed in $O(\lg{n})$ time becasue we have already discussed that the height of a red-black tree is $O(\lg{n})$. In the code to fix the violation, only case 1 is going to make the loop iterate further but not case 2 or 3 because they are making the parent of z black and the loop will only iterate if it is red.

The Case 1 is shifting z two levels up. So even if it reaches the root, it will do it in $O(\lg{n})$ time. Therefore, the total that can be taken by the entire process of insertion is still $O(\lg{n})$.

The last part to get a full-fledged working red-black tree is to delete any node from it and we will learn it in the next chapter.

If you wish to make an apple pie from scratch, you must first invent the universe

- Carl Sagan

Red-Black Trees | Insertion

Rotations in Binary Search Tree

Code of Rotations

Insertion

Code for Insertion

Code for Fixup

Analysis of Insertion