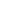Rat in a maze is also one popular problem that utilizes backtracking. If you want to brush up your concepts of backtracking, then you can read this post here. You can also see this post related to solving a Sudoku using backtracking.
A maze is a 2D matrix in which some cells are blocked. One of the cells is the source cell, from where we have to start. And another one of them is the destination, where we have to reach. We have to find a path from the source to the destination without moving into any of the blocked cells. A picture of an unsolved maze is shown below.

And this is its solution.
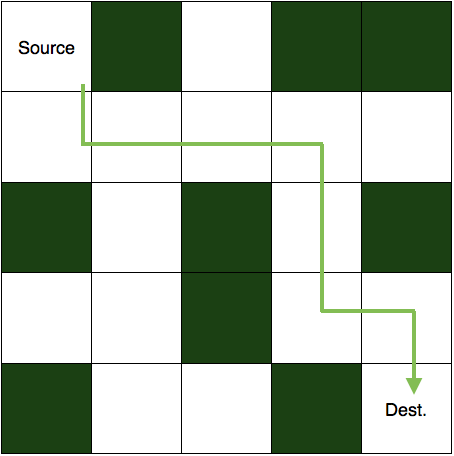
To solve this puzzle, we first start with the source cell and move in a direction where the path is not blocked. If taken path makes us reach to the destination then the puzzle is solved else, we come back and change our direction of the path taken. We are going to implement the same logic in our code also. So, let's see how.
Algorithm to solve a rat in a maze
You know about the problem, so let's see how we are going to solve it. Firstly, we will make a matrix to represent the maze, and the elements of the matrix will be either 0 or 1. 1 will represent the blocked cell and 0 will represent the cells in which we can move. The matrix for the maze shown above is:
0 1 0 1 1
0 0 0 0 0
1 0 1 0 1
0 0 1 0 0
1 0 0 1 0
Now, we will make one more matrix of the same dimension to store the solution. Its elements will also be either 0 or 1. 1 will represent the cells in our path and rest of the cells will be 0. The matrix representing the solution is:
1 0 0 0 0
1 1 1 1 0
0 0 0 1 0
0 0 0 1 1
0 0 0 0 1
Thus, we now have our matrices. Next, we will find a path from the source cell to the destination cell and the steps we will take are:
- Check for the current cell, if it is the destination cell, then the puzzle is solved.
- If not, then we will try to move downward and see if we can move in the downward cell or not (to move in a cell it must be vacant and not already present in the path).
- If we can move there, then we will continue with the path taken to the next downward cell.
- If not, we will try to move to the rightward cell. And if it is blocked or taken, we will move upward.
- Similarly, if we can't move up as well, we will simply move to the left cell.
- If none of the four moves (down, right, up, or left) are possible, we will simply move back and change our current path (backtracking).
Thus, the summary is that we try to move to the other cell (down, right, up, and left) from the current cell and if no movement is possible, then just come back and change the direction of the path to another cell.
Let's code the above algorithm and solve the puzzle.
C
#include <stdio.h>
#define SIZE 5
//the maze problem
int maze[SIZE][SIZE] = {
{0,1,0,1,1},
{0,0,0,0,0},
{1,0,1,0,1},
{0,0,1,0,0},
{1,0,0,1,0}
};
//matrix to store the solution
int solution[SIZE][SIZE];
//function to print the solution matrix
void printsolution()
{
int i,j;
for(i=0;i<SIZE;i++)
{
for(j=0;j<SIZE;j++)
{
printf("%d\t",solution[i][j]);
}
printf("\n\n");
}
}
//function to solve the maze
//using backtracking
int solvemaze(int r, int c)
{
//if destination is reached, maze is solved
//destination is the last cell(maze[SIZE-1][SIZE-1])
if((r==SIZE-1) && (c==SIZE-1))
{
solution[r][c] = 1;
return 1;
}
//checking if we can visit in this cell or not
//the indices of the cell must be in (0,SIZE-1)
//and solution[r][c] == 0 is making sure that the cell is not already visited
//maze[r][c] == 0 is making sure that the cell is not blocked
if(r>=0 && c>=0 && r<SIZE && c<SIZE && solution[r][c] == 0 && maze[r][c] == 0)
{
//if safe to visit then visit the cell
solution[r][c] = 1;
//going down
if(solvemaze(r+1, c))
return 1;
//going right
if(solvemaze(r, c+1))
return 1;
//going up
if(solvemaze(r-1, c))
return 1;
//going left
if(solvemaze(r, c-1))
return 1;
//backtracking
solution[r][c] = 0;
return 0;
}
return 0;
}
int main()
{
//making all elements of the solution matrix 0
int i,j;
for(i=0; i<SIZE; i++)
{
for(j=0; j<SIZE; j++)
{
solution[i][j] = 0;
}
}
if (solvemaze(0,0))
printsolution();
else
printf("No solution\n");
return 0;
}
Java
class Maze
{
private static final int SIZE = 5;
//the maze problem
private static int[][] maze = {
{0,1,0,1,1},
{0,0,0,0,0},
{1,0,1,0,1},
{0,0,1,0,0},
{1,0,0,1,0}
};
//matrix to store the solution
private static int[][] solution = new int[SIZE][SIZE];
//function to print the solution matrix
private static void printSolution()
{
for(int i=0;i<SIZE;i++)
{
for(int j=0;j<SIZE;j++)
{
System.out.print(solution[i][j]+"\t");
}
System.out.print("\n\n");
}
}
//function to solve the maze
//using backtracking
private static boolean solveMaze(int r, int c)
{
//if destination is reached, maze is solved
//destination is the last cell(maze[SIZE-1][SIZE-1])
if((r==SIZE-1) && (c==SIZE-1))
{
solution[r][c] = 1;
return true;
}
//checking if we can visit in this cell or not
//the indices of the cell must be in (0,SIZE-1)
//and solution[r][c] == 0 is making sure that the cell is not already visited
//maze[r][c] == 0 is making sure that the cell is not blocked
if(r>=0 && c>=0 && r<SIZE && c<SIZE && solution[r][c] == 0 && maze[r][c] == 0)
{
//if safe to visit then visit the cell
solution[r][c] = 1;
//going down
if(solveMaze(r+1, c))
return true;
//going right
if(solveMaze(r, c+1))
return true;
//going up
if(solveMaze(r-1, c))
return true;
//going left
if(solveMaze(r, c-1))
return true;
//backtracking
solution[r][c] = 0;
return false;
}
return false;
}
public static void main(String[] args)
{
if (solveMaze(0,0))
printSolution();
else
System.out.println("No solution\n");
}
}
Python
SIZE = 5
#maze problem
maze = [
[0,1,0,1,1],
[0,0,0,0,0],
[1,0,1,0,1],
[0,0,1,0,0],
[1,0,0,1,0]
]
#list to store the solution matrix
solution = [[0]*SIZE for _ in range(SIZE)]
#function to solve the maze
#using backtracking
def solvemaze(r, c):
#if destination is reached, maze is solved
#destination is the last cell(maze[SIZE-1][SIZE-1])
if (r==SIZE-1) and (c==SIZE-1):
solution[r][c] = 1;
return True;
#checking if we can visit in this cell or not
#the indices of the cell must be in (0,SIZE-1)
#and solution[r][c] == 0 is making sure that the cell is not already visited
#maze[r][c] == 0 is making sure that the cell is not blocked
if r>=0 and c>=0 and r<SIZE and c<SIZE and solution[r][c] == 0 and maze[r][c] == 0:
#if safe to visit then visit the cell
solution[r][c] = 1
#going down
if solvemaze(r+1, c):
return True
#going right
if solvemaze(r, c+1):
return True
#going up
if solvemaze(r-1, c):
return True
#going left
if solvemaze(r, c-1):
return True
#backtracking
solution[r][c] = 0;
return False;
return 0;
if(solvemaze(0,0)):
for i in solution:
print (i)
else:
print ("No solution")
Explanation of the code
printsolution → This function is just printing the solution matrix.
solvemaze → This is the actual function where we are implementing the backtracking algorithm. Firstly, we are checking of our cell is the destination cell or not if (r==SIZE-1) and (c==SIZE-1). If it is the destination cell then our puzzle is already solved. If not, then we are checking if it a valid cell to move or not. A valid cell must be in the matrix i.e., indices must between 0 to SIZE-1 r>=0 && c>=0 && r<SIZE; must not be blocked maze[r][c] == 0 and must not be taken in the path solution[r][c] == 0. If it is a valid move then we are free to take it and move to the next cell. Firstly, we will try the downward cell if(solveMaze(r+1, c)). If it doesn't give us the solution then we will move to the rightward cell, and similarly to the upward and the leftward cells. If all of the cells fail to give us the solution, we will leave the cell solution[r][c] = 0 and go to some other cell.