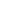Prerequisite - Heap
Priority queue is a type of queue in which every element has a key associated to it and the queue returns the element according to these keys, unlike the traditional queue which works on first come first serve basis.
Thus, a max-priority queue returns the element with maximum key first whereas, a min-priority queue returns the element with the smallest key first.

Priority queues are used in many algorithms like Huffman Codes, Prim's algorithm, etc. It is also used in scheduling processes for a computer, etc.
Heaps are great for implementing a priority queue because of the largest and smallest element at the root of the tree for a max-heap and a min-heap respectively. We use a max-heap for a max-priority queue and a min-heap for a min-priority queue.
There are mainly 4 operations we want from a priority queue:
1. Insert → To insert a new element in the queue.
2. Maximum/Minimum → To get the maximum and the minimum element from the max-priority queue and min-priority queue respectively.
3. Extract Maximum/Minimum → To remove and return the maximum and the minimum element from the max-priority queue and min-priority queue respectively.
4. Increase/Decrease key → To increase or decrease key of any element in the queue.
A priority queue stores its data in a specific order according to the keys of the elements. So, inserting a new data must go in a place according to the specified order. This is what the insert operation does.
The entire point of the priority queue is to get the data according to the key of the data and the Maximum/Minimum and Extract Maximum/Minimum does this for us.
With these operations, we have fulfilled most of our demand of a priority queue i.e., to insert data into the queue and take data from the queue. But we may also face a situation in which we need to change the key of an element, so Increase/Decrease key is used to do that.
Let's learn to code these operations to make a priority queue.
The Pseudo codes given below are for a max-priority queue. However, full code in C, Java and Python is given for both max-priority and min-priority queues at the last of this article.
As stated earlier, we are going to use a heap for the priority queue.
Maximum/Minimum
We know that the maximum (or minimum) element of a priority queue is at the root of the max-heap (or min-heap). So, we just need to return the element at the root of the heap.
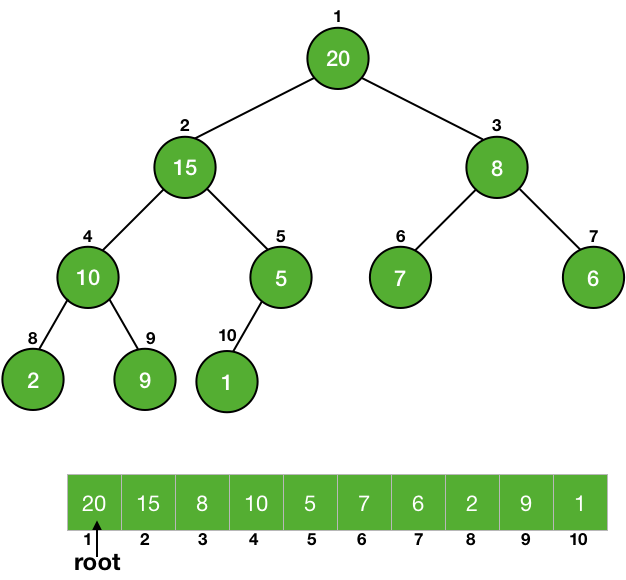
MAXIMUM(A) return A[1]
Returning an element from an array is a constant time taking process, so it is a $\Theta(1)$ process.
Extract Maximum/Minimum
This is like the pop of a queue, we return the element as well as delete it from the heap. So, we have to return and delete the root of a heap. Firstly, we store the value of the root in a variable to return it later from the function and then we just make the root equal to the last element of the heap. Now the root is equal to the last element of the heap, we delete the last element easily by reducing the size of the heap by 1.
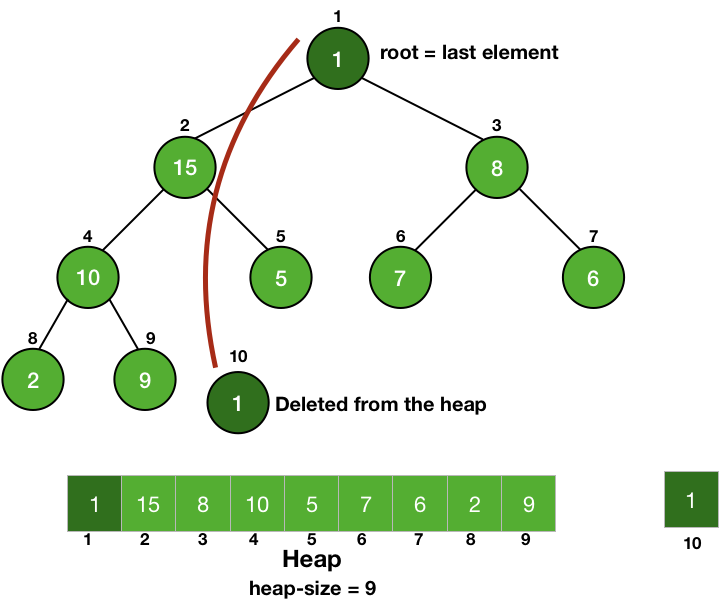
Doing this, we have disturbed the heap property of the root but we have not touched any of its children, so they are still heaps. So, we can call Heapify on the root to make the tree a heap again.
EXTRACT-MAXIMUM(A) max = A[1] // stroing maximum value A[1] = A[heap_size] // making root equal to the last element heap_size = heap_size-1 // delete last element MAX-HEAPIFY(A, 1) // root is not following max-heap property return max //returning the maximum value
All the steps are constant time taking process except the Heapify operation, it will take $O(\lg{n})$ time and thus the Extract Maximum/Minimum is going to take $O(\lg{n})$ time.
Increase/Decrease key
Whenever we change the key of an element, it must change its position to go in a place of correct order according to the new key. If the heap is a max-heap and we are decreasing the key, then we just need to check if the key became smaller than any of its children or not. If the new key is smaller than any of its children, then it is violating the heap property, so we will call Heapify on it.
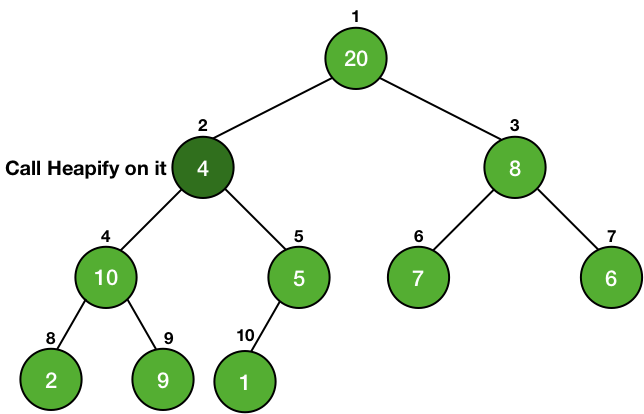
In the case of increasing the key of an element in a max-heap, we might make it greater than the key of its parent and thus violating the heap property. In this case, we swap the values of the parent and the node and this is done until the parent of the node becomes greater than the node itself.
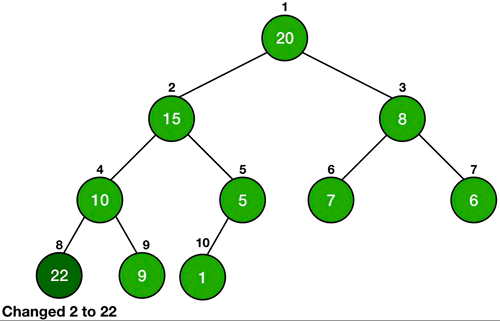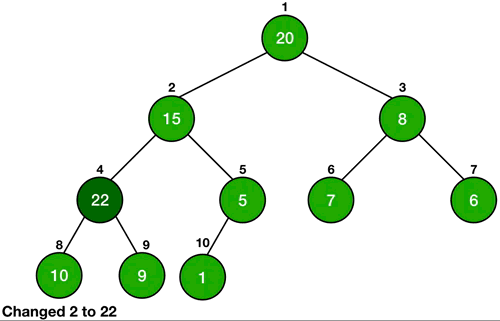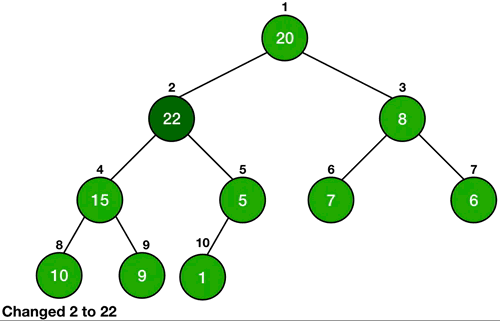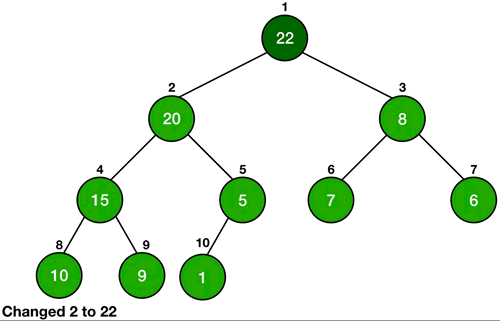
In the case of a min-queue, we do exactly the opposite of the above steps.
INCREASE-KEY(A, i, key)
A[i] = key // changing key
while i > 1 and A[Parent(i) < A[i] // if parent is less than A[i], we will swap.
swap (A[i], A[Parent(i)])
i = Parent(i)
DECREASE-KEY(A, i, key) A[i] = key // changing key MAX-HEAPIFY(A, i)
It is similar to Heapify operation. Instead of traveling down the tree, we are traveling up, so it is also going to take $\lg{n}$ time in the worst case i.e., it is an $O(\lg{n})$ operation.
Insert
The insert operation inserts a new element in the correct order according to its key. We just insert a new element at the last of the heap and increase the heap size by 1. Since it is the last element, so we first give a very large value (infinity) in the case of min-heap and a very less value (-inf) in the case of max-heap. Then we just change the key of the element by using the Increase/Decrease key operation.
INSERT(A, key) heap_size = heap_size+1 // increasing heap size by 1 A[heap_size] = -infinity // making last element very less INCREASE-KEY(A, heap_size, key) // chaning key of last element
All the steps are constant time taking steps, except the Increase/Decrease key. So it will also take $O(\lg{n})$ time.
Code for Max-Priority Queue - C, Java and Python
- C
- Python
- Java
#include <stdio.h>
int tree_array_size = 20;
int heap_size = 0;
const int INF = 100000;
void swap( int *a, int *b ) {
int t;
t = *a;
*a = *b;
*b = t;
}
//function to get right child of a node of a tree
int get_right_child(int A[], int index) {
if((((2*index)+1) < tree_array_size) && (index >= 1))
return (2*index)+1;
return -1;
}
//function to get left child of a node of a tree
int get_left_child(int A[], int index) {
if(((2*index) < tree_array_size) && (index >= 1))
return 2*index;
return -1;
}
//function to get the parent of a node of a tree
int get_parent(int A[], int index) {
if ((index > 1) && (index < tree_array_size)) {
return index/2;
}
return -1;
}
void max_heapify(int A[], int index) {
int left_child_index = get_left_child(A, index);
int right_child_index = get_right_child(A, index);
// finding largest among index, left child and right child
int largest = index;
if ((left_child_index <= heap_size) && (left_child_index>0)) {
if (A[left_child_index] > A[largest]) {
largest = left_child_index;
}
}
if ((right_child_index <= heap_size && (right_child_index>0))) {
if (A[right_child_index] > A[largest]) {
largest = right_child_index;
}
}
// largest is not the node, node is not a heap
if (largest != index) {
swap(&A[index], &A[largest]);
max_heapify(A, largest);
}
}
void build_max_heap(int A[]) {
int i;
for(i=heap_size/2; i>=1; i--) {
max_heapify(A, i);
}
}
int maximum(int A[]) {
return A[1];
}
int extract_max(int A[]) {
int maxm = A[1];
A[1] = A[heap_size];
heap_size--;
max_heapify(A, 1);
return maxm;
}
void increase_key(int A[], int index, int key) {
A[index] = key;
while((index>1) && (A[get_parent(A, index)] < A[index])) {
swap(&A[index], &A[get_parent(A, index)]);
index = get_parent(A, index);
}
}
void decrease_key(int A[], int index, int key) {
A[index] = key;
max_heapify(A, index);
}
void insert(int A[], int key) {
heap_size++;
A[heap_size] = -1*INF;
increase_key(A, heap_size, key);
}
void print_heap(int A[]) {
int i;
for(i=1; i<=heap_size; i++) {
printf("%d\n",A[i]);
}
printf("\n");
}
int main() {
int A[tree_array_size];
insert(A, 20);
insert(A, 15);
insert(A, 8);
insert(A, 10);
insert(A, 5);
insert(A, 7);
insert(A, 6);
insert(A, 2);
insert(A, 9);
insert(A, 1);
print_heap(A);
increase_key(A, 5, 22);
print_heap(A);
decrease_key(A, 1, 13);
print_heap(A);
printf("%d\n\n", maximum(A));
printf("%d\n\n", extract_max(A));
print_heap(A);
printf("%d\n", extract_max(A));
printf("%d\n", extract_max(A));
printf("%d\n", extract_max(A));
printf("%d\n", extract_max(A));
printf("%d\n", extract_max(A));
printf("%d\n", extract_max(A));
printf("%d\n", extract_max(A));
printf("%d\n", extract_max(A));
printf("%d\n", extract_max(A));
return 0;
}
Code for Min-Priority Queue - C, Java and Python
- C
- Python
- Java
#include <stdio.h>
int tree_array_size = 20;
int heap_size = 0;
const int INF = 100000;
void swap( int *a, int *b ) {
int t;
t = *a;
*a = *b;
*b = t;
}
//function to get right child of a node of a tree
int get_right_child(int A[], int index) {
if((((2*index)+1) < tree_array_size) && (index >= 1))
return (2*index)+1;
return -1;
}
//function to get left child of a node of a tree
int get_left_child(int A[], int index) {
if(((2*index) < tree_array_size) && (index >= 1))
return 2*index;
return -1;
}
//function to get the parent of a node of a tree
int get_parent(int A[], int index) {
if ((index > 1) && (index < tree_array_size)) {
return index/2;
}
return -1;
}
void min_heapify(int A[], int index) {
int left_child_index = get_left_child(A, index);
int right_child_index = get_right_child(A, index);
// finding smallest among index, left child and right child
int smallest = index;
if ((left_child_index <= heap_size) && (left_child_index>0)) {
if (A[left_child_index] < A[smallest]) {
smallest = left_child_index;
}
}
if ((right_child_index <= heap_size && (right_child_index>0))) {
if (A[right_child_index] < A[smallest]) {
smallest = right_child_index;
}
}
// smallest is not the node, node is not a heap
if (smallest != index) {
swap(&A[index], &A[smallest]);
min_heapify(A, smallest);
}
}
void build_min_heap(int A[]) {
int i;
for(i=heap_size/2; i>=1; i--) {
min_heapify(A, i);
}
}
int minimum(int A[]) {
return A[1];
}
int extract_min(int A[]) {
int minm = A[1];
A[1] = A[heap_size];
heap_size--;
min_heapify(A, 1);
return minm;
}
void decrease_key(int A[], int index, int key) {
A[index] = key;
while((index>1) && (A[get_parent(A, index)] > A[index])) {
swap(&A[index], &A[get_parent(A, index)]);
index = get_parent(A, index);
}
}
void increase_key(int A[], int index, int key) {
A[index] = key;
min_heapify(A, index);
}
void insert(int A[], int key) {
heap_size++;
A[heap_size] = INF;
decrease_key(A, heap_size, key);
}
void print_heap(int A[]) {
int i;
for(i=1; i<=heap_size; i++) {
printf("%d\n",A[i]);
}
printf("\n");
}
int main() {
int A[tree_array_size];
insert(A, 20);
insert(A, 15);
insert(A, 8);
insert(A, 10);
insert(A, 5);
insert(A, 7);
insert(A, 6);
insert(A, 2);
insert(A, 9);
insert(A, 1);
print_heap(A);
increase_key(A, 5, 22);
print_heap(A);
printf("%d\n\n", minimum(A));
printf("%d\n\n", extract_min(A));
print_heap(A);
printf("%d\n", extract_min(A));
printf("%d\n", extract_min(A));
printf("%d\n", extract_min(A));
printf("%d\n", extract_min(A));
printf("%d\n", extract_min(A));
printf("%d\n", extract_min(A));
printf("%d\n", extract_min(A));
printf("%d\n", extract_min(A));
printf("%d\n", extract_min(A));
return 0;
}