Shell Sort

Overview

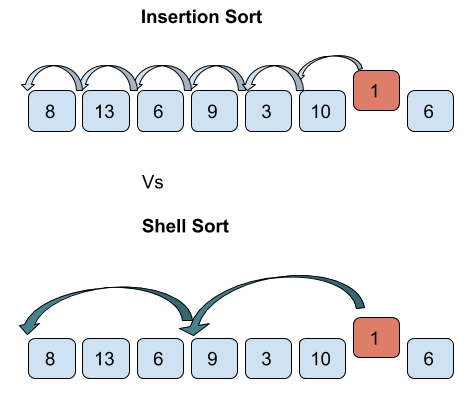
Shell Sort is based on Insertion Sort algorithm and is efficient in sorting widely placed unsorted array. Let's say, if an element in an unsorted array is much far from its sorted position, then insertion sort becomes costly as it will compare and shift one by one every element greater than it (i.e. it will take (element original position - element sorted position) number of swaps/shifts to sort that element.). See figure 1,

Shell sort addresses this problem and reduces the number of shifts/swaps by dividing the array into subarrays of intervals (gap) and then applying insertion sort on the sub-arrays. This process is repeated with reducing interval (gap) size until the gap becomes 0. As a result, the number of swaps significantly reduces but at the cost of more number of comparisons.

Algorithm of Shell Sort

1. Initialize the gap size.
2. Divide the array into subarrays of equal gap size.
3. Apply insertion sort on the subarrays.
4. Repeat the above steps until the gap size becomes 0 resulting into a sorted array.

Find below the working of shell sort for the example list = [7, 4, 9, 2, 6, 3] with starting gap size = 3 and reducing the gap size by 1 after every iteration till the gap size is greater than 0.

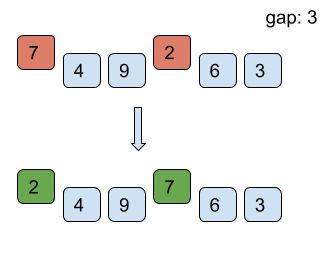
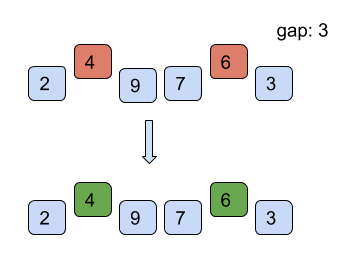
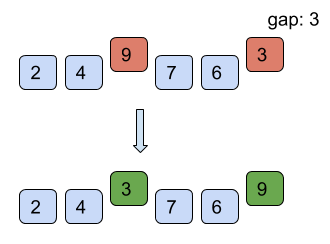
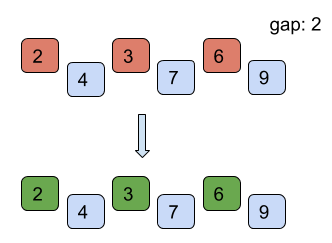
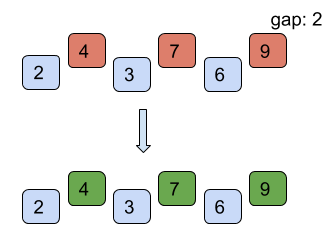
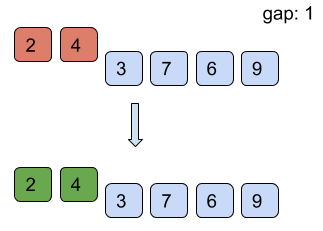
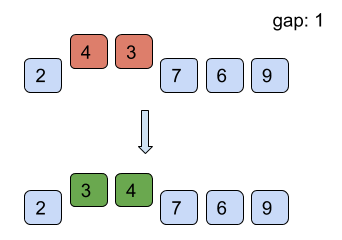
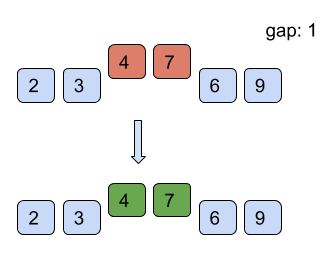
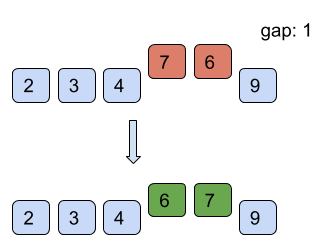
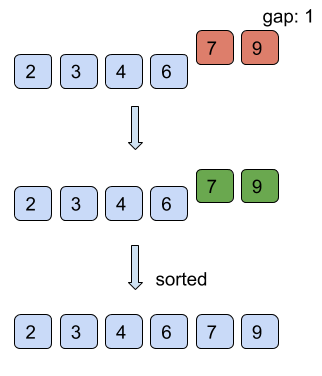
However, it is intuitive from the above example that the number of comparisons is more than those in insertion sort. However, comparisons are less costly than shifts. Therefore, insertion sort is only used where the array is almost sorted.

How to choose gap size?

The overall time complexity of the algorithm will depend on the gap sequence we use to sort the array. There is no perfect sequence that works out with every type of input data. However, there are certain proposed sequences which work out well in general case. For more such gap sequences, visit here.

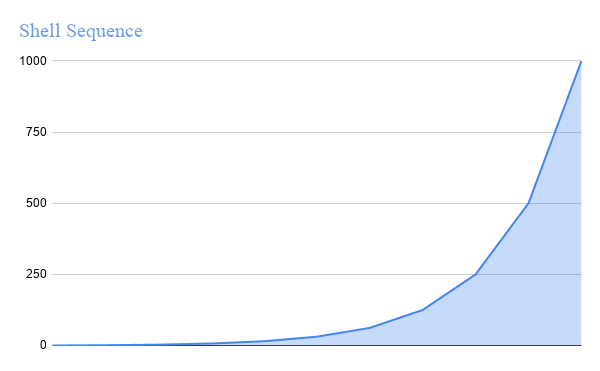
Shell Sequence

Shell Sequence is proposed by Donald Shell that follows formula $floor(\frac{N}{2^{K}})$, which results in the sequence: [500, 250, 125, 62,31, 15, 7, 3, 1] for N = 1000.

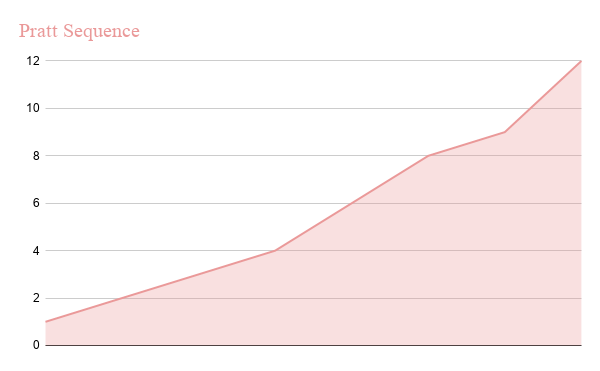
Pratt Sequence

Pratt proposed a sequence of successive numbers of the form 2^P3^Q or [1, 2, 3, 4, 6, 8, 9, 12, . . ]. This sequence grows at a slower pace than Shell sequence as seen in the figure,

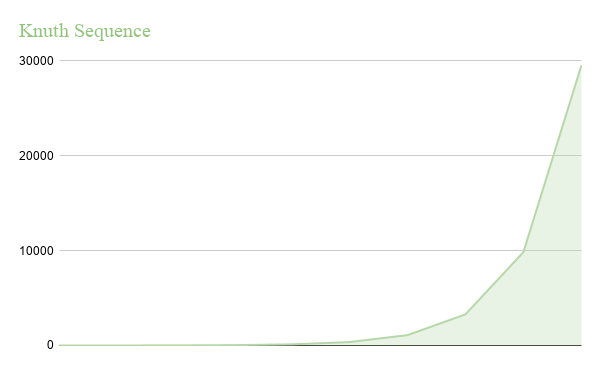
Knuth Sequence

Knuth proposes a sequence that follows the formula (3^K-1)/2, which results in the sequence: [1, 4, 14, 40, 121, …].

Pseudo-code of Shell Sort 

In this section, we will be using Shell sequence to determine the gap size.

procedure shellSort()
   arr : array of elements
   n: length of array
	
   /* calculate gap size*/
   gap = floor(n/2)
   
   while gap> 0 do:

      for i= gap; i< arr.length; i++ do:

      /* select value to be inserted */
      valueToInsert = arr[i]
      j = i;

         /*shift element towards right*/
         while j>= gap && arr[j - gap] >= valueToInsert do:
            arr[j] = arr[j - gap]
            j = j- gap
         end while

      /* insert the number at hole position */
      arr[i] = valueToInsert

      end for

   /* calculate gap size*/
   gap /= 2  

   end while
   
end procedure

Implementation of Shell Sort

• C/C++
• Python
• Java

#include <stdio.h>

void shellSort(int arr[],int n){
    int gap = n/2;
    while(gap>0)
    {
        for(int i=gap;i<n;i++)
        {
            int temp = arr[i];
            int j=i;
            while(j>=gap && arr[j-gap]>temp)
            {
                arr[j] = arr[j-gap];
                j -= gap;
            }
            arr[j] = temp;
        }
        gap = gap/2;
    }
}
int main() {
    int arr[] = {4,2,8,4,6,1};
    int n = sizeof(arr)/sizeof(arr[0]);
    shellSort(arr,n);
    for(int i=0;i<n;i++){
        printf("%d ",arr[i]);
    }
    
    return 0;
}

from math import floor


def shellSort(arr):
    n = len(arr)
    # Gap sequence
    gap = floor(n / 2)
    while gap > 0:
        for i in range(gap, n):
            temp = arr[i]
            j = i
            # Compare elements at equal gap.
            while j >= gap and temp < arr[j - gap]:
                arr[j] = arr[j - gap]
                j -= gap
            arr[j] = temp
        gap = floor(gap / 2)


arr = [3, 2, 1, 4, 6]
shellSort(arr)
print(arr)

public class MyClass {
  public static void main(String args[]) {
      int arr[] = {4,2,8,4,6,1};
      shellSort(arr);
      for(int i=0;i<arr.length;i++)
          System.out.print(arr[i]+" ");
  }
  public static void shellSort(int arr[])
  {
      int n = arr.length;
      int gap = n/2;
      while(gap>0)
      {
          for(int i=gap;i<n;i++)
          {
              int temp = arr[i];
              int j=i;
              while(j>=gap && arr[j-gap]>temp)
              {
                  arr[j] = arr[j-gap];
                  j -= gap;
              }
              arr[j] = temp;
          }
          gap = gap/2;
      }
  }
}

Complexity

From the implementation of shell sort, it is clear that the gap sequence plays a major role in determining the time complexity of the algorithm. For shell’s sequence, the time complexity is $O(n^2)$ while for Patt’s sequence it is $O(nlog^{2}n)$. And the best of all three Knuth’s sequence with time complexity $O(n^{3/2})$.