Tower of Hanoi

Tower of Hanoi is a mathematical puzzle which consists of three towers(or pegs) and n disks of different sizes, numbered from 1, the smallest disk, to n, the largest disk. These disks are stacked over one other on one of the towers in descending order of their size from bottom i.e. nth disk at the bottom and 1st disk at the top. Here’s what the tower of Hanoi looks for n=3,

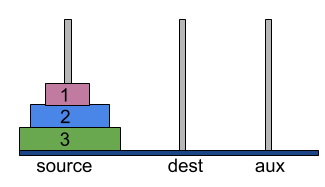
The task is to move all the disks from one tower, say source tower, to another tower, say dest tower, while following the below rules,

• You can move only one disk at a time from the top of any tower.
• No large disk should be placed over a small disk. For eg. if disk 1 is on a tower, then all the disks below it should be less than 3.

Input: n=2.

Output: Move Disk 1 from source to aux
             Move Disk 2 from source to dest
             Move Disk 1 from aux to dest

Algorithm

Let’s start the problem with n=1 disk at source tower. To solve this problem, we need to just move that disk to dest tower in one step.

And for n=3 disks,

• First, move disk 1 from source to dest tower.
  
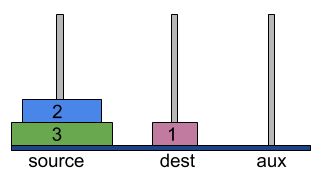
• Move disk 2 from source to aux tower.
  
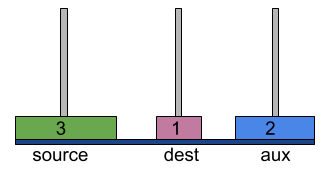
• Now move disk 1 from dest to aux tower on top of disk 2.
  
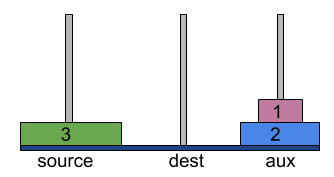
• Then, move disk 3 from source to dest tower.
  
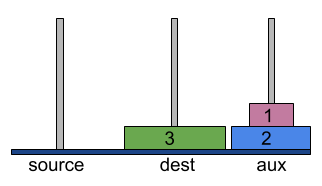
• Again Move disk 1 from aux to source tower.
  
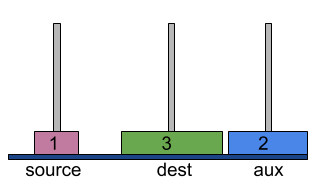
• Then move disk 2 to dest tower on top of disk 3.
  
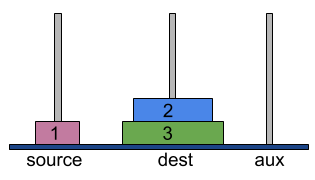
• And at last, move disk 1 to dest tower on top of 2.
  

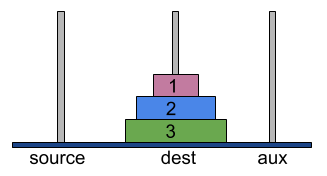
Find below the above steps in action,

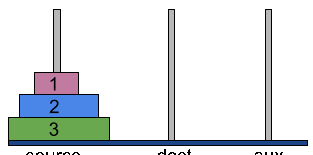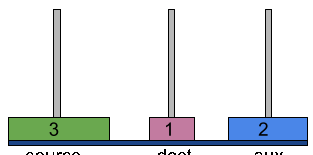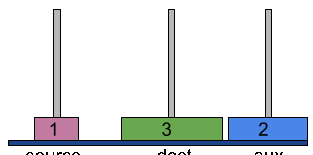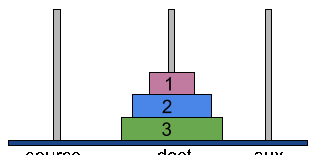
We can break down the above steps for n=3 into three major steps as follows,

1. First, move disk 1 and disk 2 from source to aux tower i.e. (move all n-1 disks from source to aux.)
2. Then, move the 3^rd disk from source to dest tower i.e. (move n^th disk from source to dest.)
3. And finally, move disk 1 and disk 2 from aux to dest tower i.e. (again move all (n-1) disks from aux to dest.

Hence, the recursive solution for Tower of Hanoi having n disks can be written as follows,

$$TowerofHanoi(n, source, dest, aux) = \text{Move disk 1 from source to dest}, \text{if $n=1$}, $$ $$ \left. \begin{array}{l} TowerofHanoi(n-1, source, dest, aux)\text{ //step1}\\ \text{Move $n^{th}$ disk from source to dest}\text{ //step2}\\ TowerofHanoi(n-1, aux, dest, source){ //step3} \end{array} \right\} $$

The Pseudo-code of the above recursive solution is shown below,

Void TowerofHanoi(n, source, dest, aux)
{
    // Base case
    if (n == 1)
    {
        Print(Move disk 1 from source to dest.) return
    }
    // Move (n-1) disks from source to aux.
    TowerofHanoi(n - 1, source, aux, dest)
    // Move nth disk from source to dest.
    Print(Move disk n from source to dest.)
    // Move (n-1) disks from aux to dest.
    TowerofHanoi(n, aux, dest, source)
}

Time Complexity Analysis of Tower of Hanoi

The simplified recurrence relation from the above recursive solution is,

$$ T(n) = \begin{cases} 1, & \text{if $n=1$} \\ 2T(n-1), & \text{if $n>1$} \end{cases} $$

Using Back substitution method T(n) = 2T(n-1) + 1 can be rewritten as,

$T(n) = 2(2T(n-2)+1)+1,\text{ putting }T(n-1) = 2T(n-2)+1$
$\therefore T(n) = 2^2 * T(n-2) + 2+ 1\qquad (1) $
$\text{Putting }T(n-2) = 2T(n-3)+1 \text{ in eq(1), we get}$
$T(n)=2^2 *(2T(n-3) + 1) + 2^1 + 1$
$\therefore T(n) = 2^3 * T(n-3) + 2^2 + 2^1 + 1$
$\text{Generalizing the above equation for $k^{th}$ time. We get,}$
$T(n) = 2^k * T(n-k) + 2^{k-1} + 2^{k-2} + ... + 2^2 + 2^1 + 1 \qquad(2)$
$\text{Taking base condition as $T(1) = 1$ and replacing $n-k = 1$},$
$\text{we get $k=n-1$}, thus putting in eq(2)$,
$T(n) = 2^{n-1} * T(1) + 2^{n-2} + 2^{n-3} + ... + 2^2+2^1+1$
$\text{The above equation is identified as GP series having a common ratio $r = 2$}$ and the sum is $2^{n}-1$
$\therefore T(n) = 2^{n}-1$

Hence, the time complexity of the recursive solution of Tower of Hanoi is O(2n) which is exponential.

Minimum steps required to move n disks

The minimum number of steps required to move n disks from source to dest is quite intuitive from the time complexity analysis and also from the raw examples as shown in the table,

From the above table, it is clear that for n disks, the minimum number of steps required are  1 + 2¹ +  2² + 2³ + .…. + 2ⁿ-1 which is a GP series having common ratio r=2 and sum = 2ⁿ - 1.

Hence, the Tower of Hanoi puzzle with n disks can be solved in minimum 2ⁿ−1 steps.

Find below the implementation of the recursive solution of Tower of Hanoi,

• C/C++
• Python
• Java

#include <stdio.h>

void TowerofHanoi(int n, char source[], char dest[], char aux[])
{
    // Base Case
    if (n == 1)
    {
        printf("\nMove disk 1 from %s to %s.", source, dest);
        return;
    }
    // Move (n-1) disks from source to aux.
    TowerofHanoi(n - 1, source, aux, dest);
    // Move nth disk from source to dest.
    printf("\nMove disk %d from %s to %s.", n, source, dest);
    // Move (n-1) disks from aux to dest.
    TowerofHanoi(n - 1, aux, dest, source);
}

int main()
{
    char source[] = "source";
    char dest[] = "dest";
    char aux[] = "aux";
    TowerofHanoi(4, source, dest, aux);
    return 0;
}

def TowerofHanoi(n, source, dest, aux):
    # Base Case
    if n == 1:
        print(f"Move disk 1 from {source} to {dest}", end="\n")
        return
    # Move (n-1) disks from source to aux.
    TowerofHanoi(n - 1, source, aux, dest)
    # Move nth disk from source to dest.
    print(f"Move disk {n} from {source} to {dest}", end="\n")
    # Move (n-1) disks from aux to dest.
    TowerofHanoi(n - 1, aux, dest, source)


TowerofHanoi(5, "source", "dest", "aux")

public class MyClass {
  public static void main(String args[]) {

    TowerofHanoi(3, "source", "dest", "aux");
  }

  public static void TowerofHanoi(int n, String source, String dest, String aux) {
    // Base Case
    if (n == 1) {
      System.out.println("Move disk 1 from " + source + " to " + dest);
      return;
    }
    // Move (n-1) disks from source to aux.
    TowerofHanoi(n - 1, source, aux, dest);
    // Move nth disk from source to dest.
    System.out.println("Move disk " + n + " from " + source + " to " + dest);
    // Move (n-1) disks from aux to dest.
    TowerofHanoi(n - 1, aux, dest, source);
  }
}