What is a Tree in Computer Science?
A tree is an important data structure of computer science which is useful for storing hierarchically ordered data. Unlike stack, queue and linear lists (arrays and linked lists) which are used to store linear data like marks of students in a class, list of tasks to be done, etc, trees are used to store non-linear data structures in a hierarchical order. A family tree is the most common example of hierarchical data. Directory structure, corporate structure, etc are also common examples of hierarchical data. The pictures given below show examples of a linear data structure as well as trees.
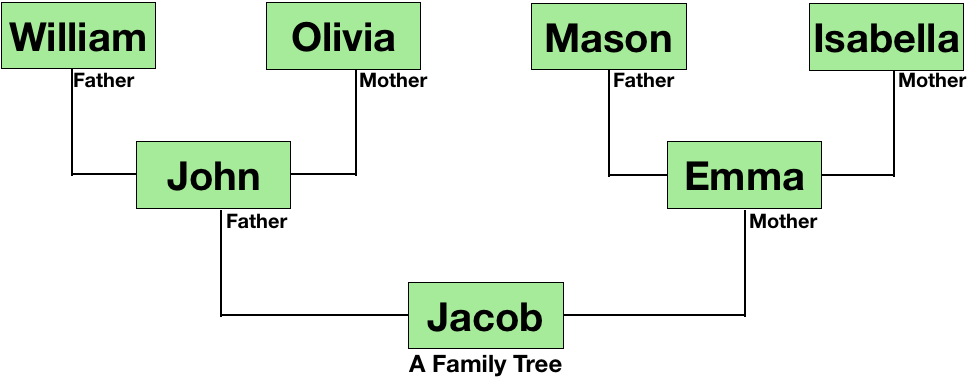
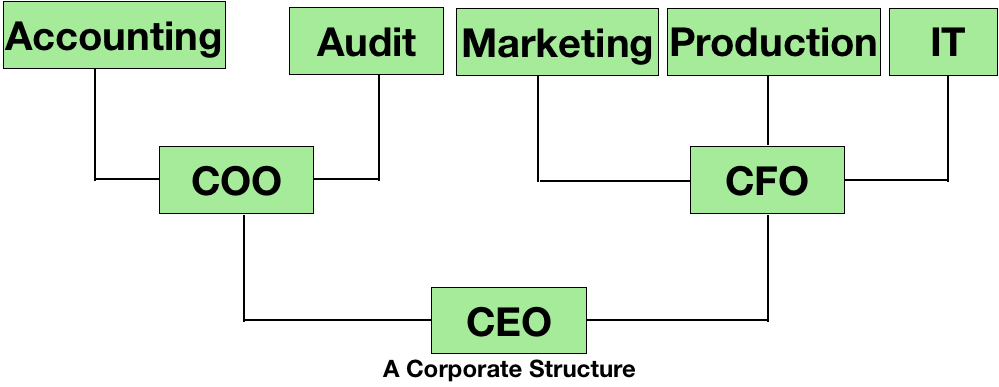
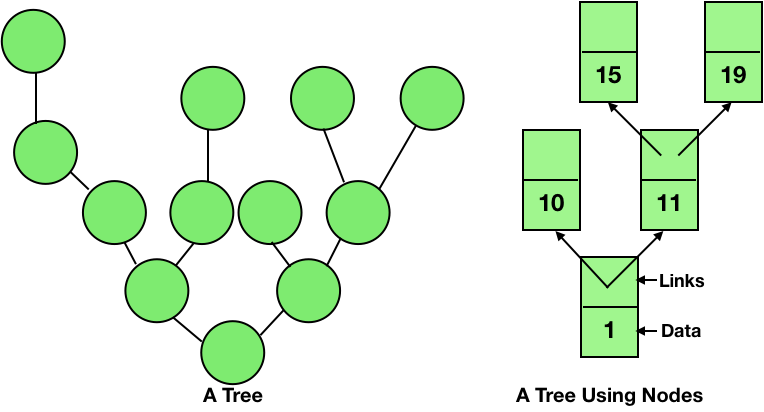
So, the next part would be to program this data structure in a programming language and use it in any project. By closely looking at the example of the corporate structure, you can see that each designation stores the name of it and contains links to the other designations; and this is a node. So, our node mainly consists of two parts - the first part stores the data (name of the designation in the above example) and the next part contains links to the other nodes (links to the sub-designations).
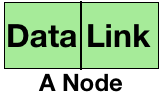
So in computer science, these nodes will be arranged in a hierarchical order to make a tree. The picture given below is a representation of a tree using nodes.
Terms Used in Tree and Properties of a Tree
Before proceeding further, you must be aware of a few terms which are listed below:
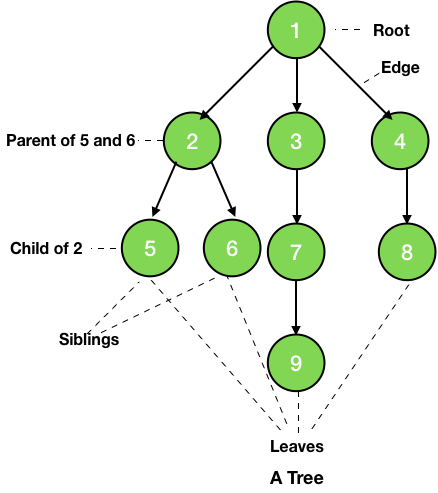
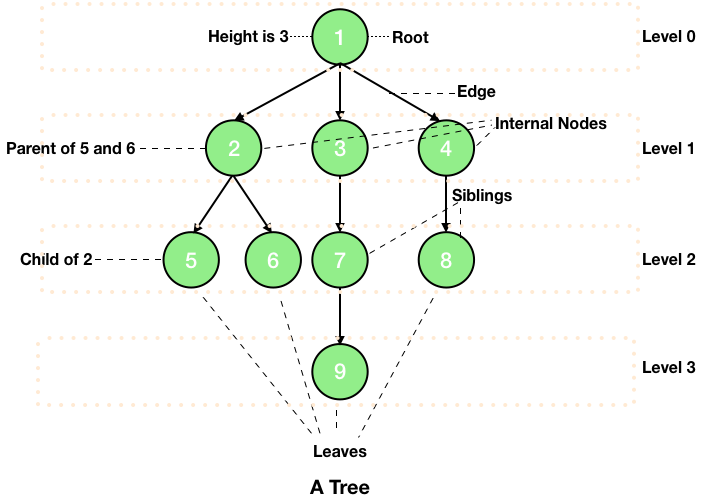
1. Root - This is the topmost node of the hierarchy or it is the node from where the tree starts. In the picture given above, 1 is the root of the tree.
2. Child - Nodes next in the hierarchy are the children of the previous node. For example, nodes 2, 3 and 4 are the children of 1.
3. Parent - The node just previous to the current node is the parent of the current node. For example, node 7 is a parent of node 9.
4. Siblings - Nodes having same parent elements are called siblings. For example, nodes 5 and 6 are siblings of each other.
5. Ancestors - Nodes which come between the path from the root to the current node are the ancestors of the current node. For example, nodes 1, 3 and 7 are the ancestors of the node 9.
6. Descendents - All the nodes which are reachable from the current node when moving downward are the descendants of the current node. For example, nodes 7 and 9 are the descendants of the node 3.
7. Internal Nodes - The nodes having at least one child are internal nodes. For example, nodes 2, 3, 4, etc are the internal nodes.
8. External Nodes/Leaves - The nodes which don't have any child or the lowest nodes are called the leaves of the tree. For example, nodes 5, 6, 9 and 8 are the leaves of the tree.
9. Edge - The link between two adjacent nodes is known as the edge.
10. Level
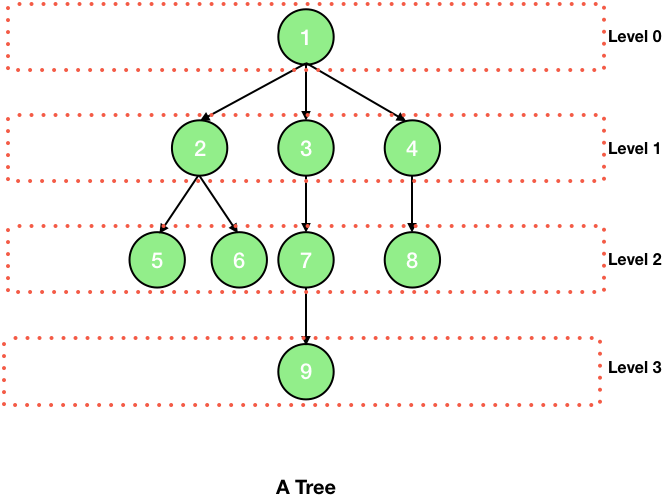
Here, the root is at level 0 and then the nodes 2, 3 and 4 are at same level 1. Thus, the level of a node is the number of edges between the path of the node and the root.
11. Height - The height of a node is the number of nodes (excluding the node) on the longest path from the node to a leaf.
12. Height of Tree - Height of a tree is the height of its root.
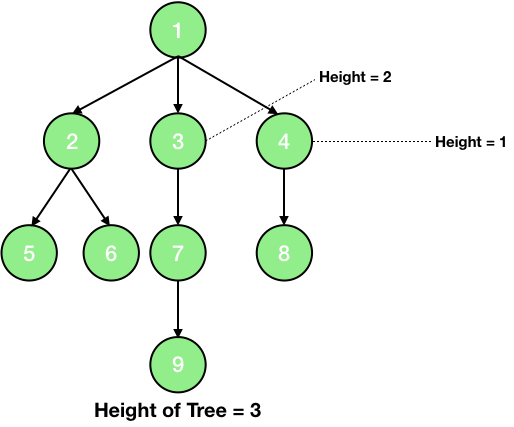
13. Depth - The depth of a node is the number of nodes (excluding the node) on the path from the root to the node.
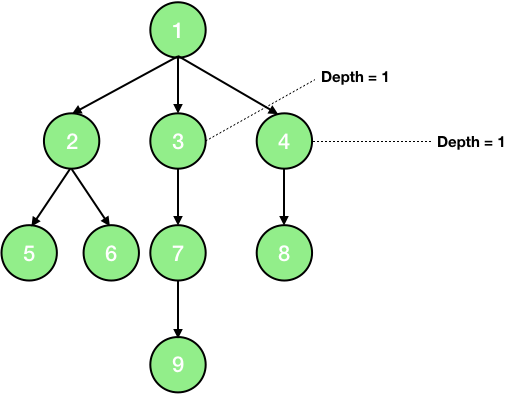
14. Node degree - It is the maximum number of children a node has.
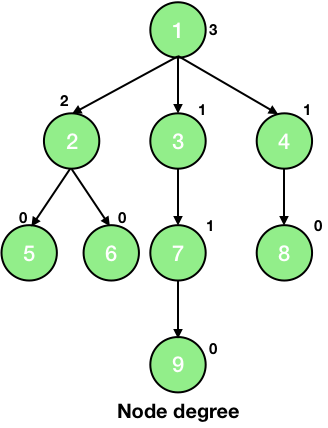
15. Tree Degree - Tree degree is the maximum of the node degrees. So, the tree degree in the above picture is 3.
Properties of a Tree
Now you know the terminology used in a tree, let's proceed further and take a look at the properties of a tree which are given below:
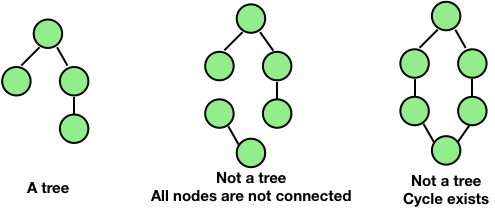
- You know that tree is a set of nodes and this set must be a finite nonempty set.
- There must exist a path to every node in the tree.
- There must not exist any cycles in the tree. It means that the number of edges is one less than the number of nodes.
Representation of a Tree in Programming Languages (C, Java and Python)
A tree is a collection of nodes and thus to program a tree, our main task is to make a node for the desired tree. For example, a binary tree consists of a maximum 2 children and thus its node will be made according to that. Here, I am just presenting an outline of how a node looks and will code up an entire tree in the next articles.
Java
class Node
{
Object element;
Node rightChild;
Node leftChild;
Node parent;
}
Here, the Object is the datatype we want to store. It can be an integer, a string, an object of a class, etc. It also has links to the other nodes, its children, and parent.
Python
class Tree:
def __init__(self, element):
self.element = element
self.right_child = none
self.left_child = none
self.parent = none
The element is the data we want to store and right_child, left_child, and parent are the links to the other nodes.
C
struct node
{
int data;
struct node *right_child;
struct node *left_child;
struct node *parent;
}
Here, the data can be of any other datatype and not just an integer. The other data members are the pointer to a node (same structure) and thus are links to the children and parent.







