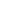Binary Trees : Classification and Traversals Using Array and Linked List

A binary tree is a tree in which every node has at most two children.

bianry tree

As you can see in the picture given above, a node can have less than 2 children but not more than that.

We can also classify a binary tree into different categories. Let's have a look at them:

Full Binary Tree → A binary tree in which every node has 2 children except the leaves is known as a full binary tree.

full bianry tree

Complete Binary Tree → A binary tree which is completely filled with a possible exception at the bottom level i.e., the last level may not be completely filled and the bottom level is filled from left to right.

complete bianry tree

Let's look at this picture to understand the difference between a full and a complete binary tree.

difference in full and complete bianry trees

A complete binary tree also holds some important properties. So, let's look at them.

The parent of node i is $\left\lfloor\frac{i}{2}\right\rfloor$. For example, the parent of node 4 is 2 and the parent of node 5 is also 2.
The left child of node i is $2i$.
The right child of node i is $2i+1$

property of bianry tree

Perfect Binary Tree → In a perfect binary tree, each leaf is at the same level and all the interior nodes have two children.

perfect bianry tree

Thus, a perfect binary tree will have the maximum number of nodes for all alternative binary trees of the same height and it will be $2^{h+1}-1$ which we are going to prove next.

Maximum Number of Nodes in a Binary Tree

We know that the maximum number of nodes will be in a perfect binary tree. So, let's assume that the height of a perfect binary tree is $h$.

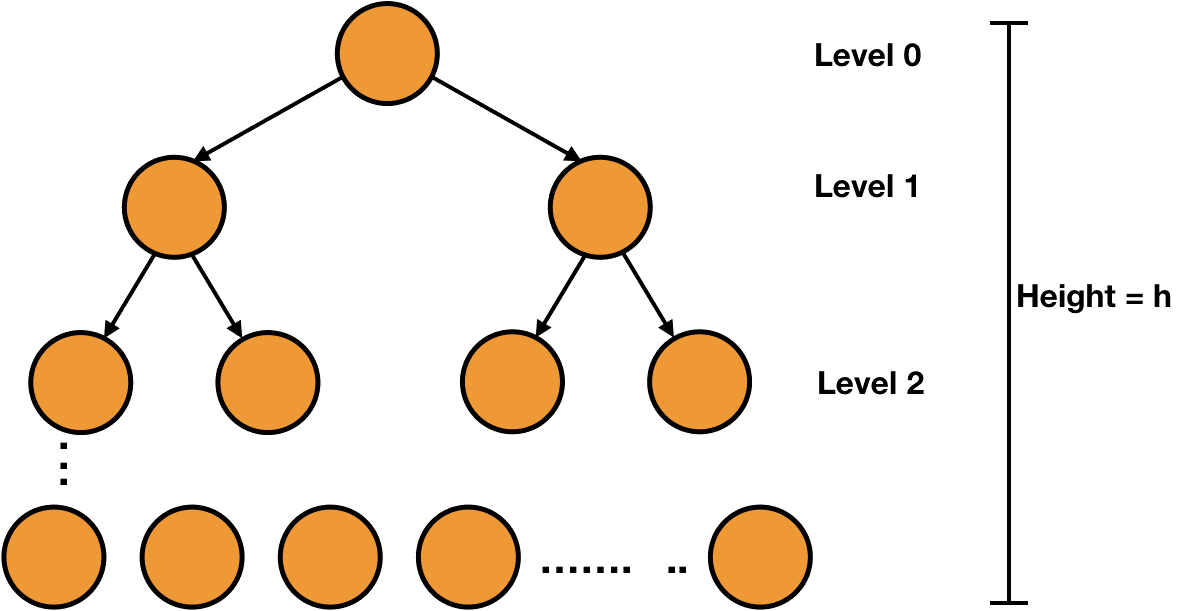
height of bianry tree

Number of nodes at level 0 = $2^{0} = 1$

Number of nodes at level 1 = $2^{1} = 2$

Similarly, the number of nodes at level h = $2^{h}$

Thus, the total number of nodes in the tree = $2^{0} + 2^{1} + ... + 2^{h}$

The above sequence is a G.P. with common ratio 2 and first term 1 and total number of terms are h+1. So, the value of the summation will be $\frac{2^{h+1}-1}{2-1} = 2^{h+1}-1$.

Thus, the total number of nodes in a perfect binary tree = $2^{h+1}-1$.

Height of a Perfect Binary Tree

We know that the number of nodes (n) for height (h) of a perfect binary tree = $2^{h+1}-1$.

$=> n = 2*2^{h}-1$

$or, 2^{h} = \frac{n+1}{2}$

$h = \lg{\frac{n+1}{2}}$

Thus, the height of a perfect binary tree with n nodes = $\lg{\frac{n+1}{2}}$.

We know that the number of nodes at level i in a perfect binary tree = $2^{i}$. Thus, the number of leaves (nodes at level h) = $2^{h}$.

Thus, the total number of non-leaf nodes = $2^{h+1}-1-2^{h} = 2^{h}-1$ i.e., number of leaf nodes - 1.

Thus, the maximum number of nodes will be in a perfect binary tree and the minimum number of nodes will be in a tree in which nodes are linked just like a linked list.

maximum and minimum number of nodes in bianry tree

Array Representation of Binary Tree

In the previous chapter, we have already seen to make a node of a tree. We can easily use those nodes to make a linked representation of a binary tree. For now, let's discuss the array representation of a binary tree.

We start by numbering the nodes of the tree from 1 to n(number of nodes).

numbering of nodes in bianry tree

As you can see, we have numbered from top to bottom and left to right for the same level. Now, these numbers represent the indices of an array (starting from 1) as shown in the picture given below.

array representation of bianry tree

We can also get the parent, the right child and the left child using the properties of a complete binary tree we have discussed above i.e., for a node i, the parent is $\left\lfloor\frac{i}{2}\right\rfloor$, the left child is $2i$ and the right child is $2i+1$.

parent and child of bianry tree

So, we represented a complete binary tree using an array and saw how to get the parent and children of any node. Let's discuss about doing the same for an incomplete binary tree.

Array Representation of Incomplete Binary Tree

To represent an incomplete binary tree with an array, we first assume that all the nodes are present to make it a complete binary tree and then number the nodes as shown in the picture given below.

incomplete bianry tree

Now according to these numbering, we fill up the array.

array representation of bianry tree

Coding a Binary Tree

For the linked representation, we can easily access the parent, right child and the left child with T.parent, T.right and T.left respectively.

So, we will first write explain the codes for the array representation and then write the full codes in C, Java and Python for both array and linked representation.

Let's start by writing the code to get the right child of a node. We will pass the index and the tree to the function - RIGHT_CHILD(index).

After this, we will check if there is a node at the index or not (if (T[index] != null)) and also if the index of the right child ($2*index + 1$) lies in the size of the tree or not i.e., if (T[index] != null and (2*index + 1) <= T.size).

If the above condition is true, we will return the index of the right child i.e., return (2*index + 1).

RIGHT_CHILD(index)
  if (T[index] != null and (2*index + 1) <= T.size)
      return (2*index + 1)
  else
      return null

Similarly, we can get the left child.

LEFT_CHILD(index)
  if (T[index] != null and (2*index) <= T.size)
      return (2*index)
  else
      return null

Similarly, we can also write the code to get the parent.

PARENT(index)
  if (T[index] != null and (floor(index/2)) =! null)
      return floor(index/2)
  else
      return null

Code Using Array

C
Python
Java

#include <stdio.h>

/*

         D
        / \
       /   \
      /     \
     A       F
    / \     / \
   /   \   /   \
  E     B R     T
 / \     /     / \
G   Q   V     J   L
*/

// variable to store maximum number of nodes
int complete_node = 15;

// array to store the tree
char tree[] = {'\0', 'D', 'A', 'F', 'E', 'B', 'R', 'T', 'G', 'Q', '\0', '\0', 'V', '\0', 'J', 'L'};

int get_right_child(int index)
{
// node is not null
// and the result must lie within the number of nodes for a complete binary tree
if(tree[index]!='\0' && ((2*index)+1)<=complete_node)
  return (2*index)+1;
// right child doesn't exist
return -1;
}

int get_left_child(int index)
{
// node is not null
// and the result must lie within the number of nodes for a complete binary tree
if(tree[index]!='\0' && (2*index)<=complete_node)
  return 2*index;
// left child doesn't exist
return -1;
}

int get_parent(int index)
{
if(tree[index]!='\0' && index/2!='\0')
  return index/2;
else
  return -1;
}

'''

         D
        / \
       /   \
      /     \
     A       F
    / \     / \
   /   \   /   \
  E     B R     T
 / \     /     / \
G   Q   V     J   L
'''

complete_node = 15

tree = [None, 'D', 'A', 'F', 'E', 'B', 'R', 'T', 'G', 'Q', None, None, 'V', None, 'J', 'L']

def get_right_child(index):
# node is not null
# and the result must lie within the number of nodes for a complete binary tree
if tree[index]!=None and ((2*index)+1)<=complete_node:
  return (2*index)+1
# right child doesn't exist
return -1

def get_left_child(index):
# node is not null
# and the result must lie within the number of nodes for a complete binary tree
if tree[index]!=None and (2*index)<=complete_node:
  return 2*index
# left child doesn't exist
return -1

def get_parent(index):
if tree[index]!=None and index/2!=None:
    return index//2
return -1

class BinaryTreeArray {
/*

         D
        / \
       /   \
      /     \
     A       F
    / \     / \
   /   \   /   \
  E     B R     T
 / \     /     / \
G   Q   V     J   L
*/

public static int completeNode = 15;

// array to store the tree
public static char tree[] = {'\0', 'D', 'A', 'F', 'E', 'B', 'R', 'T', 'G', 'Q', '\0', '\0', 'V', '\0', 'J', 'L'};

public static int getRightChild(int index) {
  // node is not null
  // and the result must lie within the number of nodes for a complete binary tree
  if(tree[index]!='\0' && ((2*index)+1)<=completeNode)
    return (2*index)+1;
  // right child doesn't exist
  return -1;
}

public static int getLeftChild(int index) {
  // node is not null
  // and the result must lie within the number of nodes for a complete binary tree
  if(tree[index]!='\0' && (2*index)<=completeNode)
    return 2*index;
  // left child doesn't exist
  return -1;
}

public static int getParent(int index) {
  if(tree[index]!='\0' && index/2!='\0')
    return index/2;
  else
    return -1;
}
}

Code Using Linked Representation

C
Python
Java

#include <stdio.h>
#include <stdlib.h>

typedef struct tree_node {
char data;
struct tree_node *right;
struct tree_node *left;
struct tree_node *parent;
}tree_node;

tree_node* new_tree_node(char data) {
tree_node *n = malloc(sizeof(tree_node));
n->data = data;
n->right = NULL;
n->left = NULL;
n->parent = NULL;

return n;
}

typedef struct tree {
tree_node *root;
}tree;

tree* new_tree(tree_node *n) {
tree *t = malloc(sizeof(tree));
t->root = n;

return t;
}

int main() {
/*

         D
        / \
       /   \
      /     \
     A       F
    / \     / \
   /   \   /   \
  E     B R     T
 / \     /     / \
G   Q   V     J   L
*/

tree_node *d, *a, *f, *e, *b, *r, *t1, *g, *q, *v, *j, *l;
d = new_tree_node('D');
a = new_tree_node('A');
f = new_tree_node('F');
e = new_tree_node('E');
b = new_tree_node('B');
r = new_tree_node('R');
t1 = new_tree_node('T');
g = new_tree_node('G');
q = new_tree_node('Q');
v = new_tree_node('V');
j = new_tree_node('J');
l = new_tree_node('L');

tree *t = new_tree(d);

t->root->right = f;
t->root->left = a;

/*

       D
      / \
     /   \
    /     \
   A       F
*/

a->right = b;
a->left = e;

f->right = t1;
f->left = r;

e->right = q;
e->left = g;

r->left = v;

t1->right = l;
t1->left = j;

return 0;
}

class TreeNode:
def __init__(self, data):
  self.data = data
  self.right = None
  self.left = None
  self.parent = None

class Tree:
def __init__(self, n):
  self.root = n

if __name__ == '__main__':
'''

             D
            / \
           /   \
          /     \
         A       F
        / \     / \
       /   \   /   \
      E     B R     T
     / \     /     / \
    G   Q   V     J   L
'''

d = TreeNode('D')
a = TreeNode('A')
f = TreeNode('F')
e = TreeNode('E')
b = TreeNode('B')
r = TreeNode('R')
t1 = TreeNode('T')
g = TreeNode('G')
q = TreeNode('Q')
v = TreeNode('V')
j = TreeNode('J')
l = TreeNode('L')

t = Tree(d)

t.root.right = f
t.root.left = a

'''

       D
      / \
     /   \
    /     \
   A       F
'''

a.right = b
a.left = e

f.right = t1
f.left = r

e.right = q
e.left = g

r.left = v

t1.right = l
t1.left = j

class TreeNode {
public char data;
public TreeNode right;
public TreeNode left;
public TreeNode parent;

public TreeNode(char data) {
  this.data = data;
  this.right = null;
  this.left = null;
  this.parent = null;
}
}

class Tree {
public TreeNode root;

public Tree(TreeNode n) {
  this.root = n;
}

public static void main(String[] args) {
  /*

             D
            / \
           /   \
          /     \
         A       F
        / \     / \
       /   \   /   \
      E     B R     T
     / \     /     / \
    G   Q   V     J   L
  */

  TreeNode d, a, f, e, b, r, t1, g, q, v, j, l;
  d = new TreeNode('D');
  a = new TreeNode('A');
  f = new TreeNode('F');
  e = new TreeNode('E');
  b = new TreeNode('B');
  r = new TreeNode('R');
  t1 = new TreeNode('T');
  g = new TreeNode('G');
  q = new TreeNode('Q');
  v = new TreeNode('V');
  j = new TreeNode('J');
  l = new TreeNode('L');

  Tree t = new Tree(d);

  t.root.right = f;
  t.root.left = a;

  /*

         D
        / \
       /   \
      /     \
     A       F
  */

  a.right = b;
  a.left = e;

  f.right = t1;
  f.left = r;

  e.right = q;
  e.left = g;

  r.left = v;

  t1.right = l;
  t1.left = j;
}
}

Binary Tree Traversal

We are ready with a binary tree. Our next task would be to visit each node of it i.e., to traverse over the entire tree. In a linear data structure like linked list, it was a simple task, we just had to visit the next pointer of the node. But since a tree is a non-linear data structure, we follow different approaches. Generally, there are three types of traversals:

Preorder Traversal
Postorder Traversal
Inorder Traversal

Basically, each of these traversals gives us a sequence in which we should visit the nodes. For example, in preorder traversal we first visit the root, then the left subtree and then the right subtree. Each traversal is useful in solving some specific problems. So, we choose the method of traversal accroding to the need of the problem we are going to solve. Let's discuss each of them one by one.

Preorder Traversal

In preorder traversal, we first visit the root of a tree, then its left subtree and after visiting the left subtree, the right subtree.

PREORDER(n)
  if(n != null)
      print(n.data) // visiting root
      PREORDER(n.left) // visiting left subtree
      PREORDER(n.right) // visiting right subtree

So, we are first checking if the node is null or not - if(n != null).

After this, we are visiting the root i.e., printing its data - print(n.data).

Then we are visiting the left subtree - PREORDER(n.left).

At last, we are visiting the right subtree - PREORDER(n.right).

So, we will first visit the root as shown in the picture given below.

preorder of bianry tree

Then, we will visit the left subtree.

preorder of bianry tree

In this left subtree, again we will visit its root and then its left subtree.

preorder of bianry tree

At last, we will visit the right subtree.

preorder of bianry tree

Postorder Traversal

In postorder traversal, we first visit the left subtree, then the right subtree and at last, the root.

POSTORDER(n)
  if(n != null)
      PREORDER(n.left) // visiting left subtree
      PREORDER(n.right) // visiting right subtree
      print(n.data) // visiting root

We will first visit the left subtree.

postorder of bianry tree

When there is no left subtree, we will visit the right subtree.

postorder of bianry tree

Since the right subtree is null, we will visit the root.

postorder of bianry tree

Similarly, we will visit every other node.

postorder of bianry tree

Inorder Traversal

In inorder traversal, we first visit the left subtree, then the root and lastly, the right subtree.

INORDER(n)
  if(n != null)
      INORDER(n.left)
      print(n.data)
      INORDER(n.right)

inorder of bianry tree

We can also see the inorder traversal as projection of the tree on an array as shown in the picture given below.

inorder of bianry tree

Code Using Array

C
Python
Java

#include <stdio.h>

/*

         D
        / \
       /   \
      /     \
     A       F
    / \     / \
   /   \   /   \
  E     B R     T
 / \     /     / \
G   Q   V     J   L
*/

// variable to store maximum number of nodes
int complete_node = 15;

// array to store the tree
char tree[] = {'\0', 'D', 'A', 'F', 'E', 'B', 'R', 'T', 'G', 'Q', '\0', '\0', 'V', '\0', 'J', 'L'};

int get_right_child(int index)
{
// node is not null
// and the result must lie within the number of nodes for a complete binary tree
if(tree[index]!='\0' && ((2*index)+1)<=complete_node)
  return (2*index)+1;
// right child doesn't exist
return -1;
}

int get_left_child(int index)
{
// node is not null
// and the result must lie within the number of nodes for a complete binary tree
if(tree[index]!='\0' && (2*index)<=complete_node)
  return 2*index;
// left child doesn't exist
return -1;
}

int get_parent(int index)
{
if(tree[index]!='\0' && index/2!='\0')
  return index/2;
else
  return -1;
}

void preorder(int index)
{
// checking for valid index and null node
if(index>0 && tree[index]!='\0')
{
  printf(" %c ",tree[index]); // visiting root
  preorder(get_left_child(index)); //visiting left subtree
  preorder(get_right_child(index)); //visiting right subtree
}
}

void postorder(int index)
{
// checking for valid index and null node
if(index>0 && tree[index]!='\0')
{
  postorder(get_left_child(index)); //visiting left subtree
  postorder(get_right_child(index)); //visiting right subtree
  printf(" %c ",tree[index]); //visiting root
}
}

void inorder(int index)
{
// checking for valid index and null node
if(index>0 && tree[index]!='\0')
{
  inorder(get_left_child(index)); //visiting left subtree
  printf(" %c ",tree[index]); //visiting root
  inorder(get_right_child(index)); // visiting right subtree
}
}

int main()
{
printf("Preorder:\n");
preorder(1);
printf("\nPostorder:\n");
postorder(1);
printf("\nInorder:\n");
inorder(1);
printf("\n");
return 0;
}

'''

         D
        / \
       /   \
      /     \
     A       F
    / \     / \
   /   \   /   \
  E     B R     T
 / \     /     / \
G   Q   V     J   L
'''

complete_node = 15

tree = [None, 'D', 'A', 'F', 'E', 'B', 'R', 'T', 'G', 'Q', None, None, 'V', None, 'J', 'L']

def get_right_child(index):
# node is not null
# and the result must lie within the number of nodes for a complete binary tree
if tree[index]!=None and ((2*index)+1)<=complete_node:
  return (2*index)+1
# right child doesn't exist
return -1

def get_left_child(index):
# node is not null
# and the result must lie within the number of nodes for a complete binary tree
if tree[index]!=None and (2*index)<=complete_node:
  return 2*index
# left child doesn't exist
return -1

def get_parent(index):
if tree[index]!=None and index/2!=None:
    return index//2
return -1

def preorder(index):
# checking for valid index and null node
if index>0 and tree[index]!=None:
  print(" "+tree[index]+" ") # visiting root
  preorder(get_left_child(index)) #visiting left subtree
  preorder(get_right_child(index)) #visiting right subtree

def postorder(index):
# checking for valid index and null node
if index>0 and tree[index]!=None:
  postorder(get_left_child(index)) #visiting left subtree
  postorder(get_right_child(index)) #visiting right subtree
  print(" "+tree[index]+" ") #visiting root

def inorder(index):
# checking for valid index and null node
if index>0 and tree[index]!=None:
  inorder(get_left_child(index)) #visiting left subtree
  print(" "+tree[index]+" ") #visiting root
  inorder(get_right_child(index)) # visiting right subtree

if __name__ == '__main__':
print("Preorder:\n")
preorder(1)
print("\nPostorder:\n")
postorder(1)
print("\nInorder:\n")
inorder(1)
print("\n")

class BinaryTreeArray {
/*

         D
        / \
       /   \
      /     \
     A       F
    / \     / \
   /   \   /   \
  E     B R     T
 / \     /     / \
G   Q   V     J   L
*/

public static int completeNode = 15;

// array to store the tree
public static char tree[] = {'\0', 'D', 'A', 'F', 'E', 'B', 'R', 'T', 'G', 'Q', '\0', '\0', 'V', '\0', 'J', 'L'};

public static int getRightChild(int index) {
  // node is not null
  // and the result must lie within the number of nodes for a complete binary tree
  if(tree[index]!='\0' && ((2*index)+1)<=completeNode)
    return (2*index)+1;
  // right child doesn't exist
  return -1;
}

public static int getLeftChild(int index) {
  // node is not null
  // and the result must lie within the number of nodes for a complete binary tree
  if(tree[index]!='\0' && (2*index)<=completeNode)
    return 2*index;
  // left child doesn't exist
  return -1;
}

public static int getParent(int index) {
  if(tree[index]!='\0' && index/2!='\0')
    return index/2;
  else
    return -1;
}

public static void preorder(int index) {
  // checking for valid index and null node
  if(index>0 && tree[index]!='\0')
  {
    System.out.print(" "+tree[index]+" "); // visiting root
    preorder(getLeftChild(index)); //visiting left subtree
    preorder(getRightChild(index)); //visiting right subtree
  }
}

public static void postorder(int index) {
  // checking for valid index and null node
  if(index>0 && tree[index]!='\0')
  {
    postorder(getLeftChild(index)); //visiting left subtree
    postorder(getRightChild(index)); //visiting right subtree
    System.out.print(" "+tree[index]+" "); //visiting root
  }
}

public static void inorder(int index) {
  // checking for valid index and null node
  if(index>0 && tree[index]!='\0')
  {
    inorder(getLeftChild(index)); //visiting left subtree
    System.out.print(" "+tree[index]+" "); //visiting root
    inorder(getRightChild(index)); // visiting right subtree
  }
}

public static void main(String[] args) {
  System.out.print("Preorder:\n");
  preorder(1);
  System.out.print("\nPostorder:\n");
  postorder(1);
  System.out.print("\nInorder:\n");
  inorder(1);
  System.out.print("\n");
}
}

Code Using Linked List

C
Python
Java

#include <stdio.h>
#include <stdlib.h>

typedef struct tree_node {
char data;
struct tree_node *right;
struct tree_node *left;
struct tree_node *parent;
}tree_node;

tree_node* new_tree_node(char data) {
tree_node *n = malloc(sizeof(tree_node));
n->data = data;
n->right = NULL;
n->left = NULL;
n->parent = NULL;

return n;
}

typedef struct tree {
tree_node *root;
}tree;

tree* new_tree(tree_node *n) {
tree *t = malloc(sizeof(tree));
t->root = n;

return t;
}

void preorder(tree_node *n) {
if(n != NULL) {
  printf(" %c ",n->data);
  preorder(n->left);
  preorder(n->right);
}
}

void postorder(tree_node *n) {
if(n != NULL) {
  postorder(n->left);
  postorder(n->right);
  printf(" %c ",n->data);
}
}

void inorder(tree_node *n) {
if(n != NULL) {
  inorder(n->left);
  printf(" %c ",n->data);
  inorder(n->right);
}
}

int main() {
/*

         D
        / \
       /   \
      /     \
     A       F
    / \     / \
   /   \   /   \
  E     B R     T
 / \     /     / \
G   Q   V     J   L
*/

tree_node *d, *a, *f, *e, *b, *r, *t1, *g, *q, *v, *j, *l;
d = new_tree_node('D');
a = new_tree_node('A');
f = new_tree_node('F');
e = new_tree_node('E');
b = new_tree_node('B');
r = new_tree_node('R');
t1 = new_tree_node('T');
g = new_tree_node('G');
q = new_tree_node('Q');
v = new_tree_node('V');
j = new_tree_node('J');
l = new_tree_node('L');

tree *t = new_tree(d);

t->root->right = f;
t->root->left = a;

/*

       D
      / \
     /   \
    /     \
   A       F
*/

a->right = b;
a->left = e;

f->right = t1;
f->left = r;

e->right = q;
e->left = g;

r->left = v;

t1->right = l;
t1->left = j;

printf("Preorder:\n");
preorder(t->root);
printf("\nPostorder:\n");
postorder(t->root);
printf("\nInorder:\n");
inorder(t->root);
printf("\n");

return 0;
}

class TreeNode:
def __init__(self, data):
  self.data = data
  self.right = None
  self.left = None
  self.parent = None

class Tree:
def __init__(self, n):
  self.root = n

def preorder(n):
if n!=None:
  print(" "+n.data+" ")
  preorder(n.left)
  preorder(n.right)

def postorder(n):
if n!=None:
  postorder(n.left)
  postorder(n.right)
  print(" "+n.data+" ")

def inorder(n):
if n!=None:
  inorder(n.left)
  print(" "+n.data+" ")
  inorder(n.right)

if __name__ == '__main__':
'''

             D
            / \
           /   \
          /     \
         A       F
        / \     / \
       /   \   /   \
      E     B R     T
     / \     /     / \
    G   Q   V     J   L
'''

d = TreeNode('D')
a = TreeNode('A')
f = TreeNode('F')
e = TreeNode('E')
b = TreeNode('B')
r = TreeNode('R')
t1 = TreeNode('T')
g = TreeNode('G')
q = TreeNode('Q')
v = TreeNode('V')
j = TreeNode('J')
l = TreeNode('L')

t = Tree(d)

t.root.right = f
t.root.left = a

'''

       D
      / \
     /   \
    /     \
   A       F
'''

a.right = b
a.left = e

f.right = t1
f.left = r

e.right = q
e.left = g

r.left = v

t1.right = l
t1.left = j

print("Preorder:\n")
preorder(t.root)
print("\nPostorder:\n")
postorder(t.root)
print("\nInorder:\n");
inorder(t.root)
print("\n")

class TreeNode {
public char data;
public TreeNode right;
public TreeNode left;
public TreeNode parent;

public TreeNode(char data) {
  this.data = data;
  this.right = null;
  this.left = null;
  this.parent = null;
}
}

class Tree {
public TreeNode root;

public Tree(TreeNode n) {
  this.root = n;
}

public static void preorder(TreeNode n) {
  if(n != null) {
    System.out.print(" "+n.data+" ");
    preorder(n.left);
    preorder(n.right);
  }
}

public static void postorder(TreeNode n) {
  if(n != null) {
    postorder(n.left);
    postorder(n.right);
    System.out.print(" "+n.data+" ");
  }
}

public static void inorder(TreeNode n) {
  if(n != null) {
    inorder(n.left);
    System.out.print(" "+n.data+" ");
    inorder(n.right);
  }
}

public static void main(String[] args) {
  /*

             D
            / \
           /   \
          /     \
         A       F
        / \     / \
       /   \   /   \
      E     B R     T
     / \     /     / \
    G   Q   V     J   L
  */

  TreeNode d, a, f, e, b, r, t1, g, q, v, j, l;
  d = new TreeNode('D');
  a = new TreeNode('A');
  f = new TreeNode('F');
  e = new TreeNode('E');
  b = new TreeNode('B');
  r = new TreeNode('R');
  t1 = new TreeNode('T');
  g = new TreeNode('G');
  q = new TreeNode('Q');
  v = new TreeNode('V');
  j = new TreeNode('J');
  l = new TreeNode('L');

  Tree t = new Tree(d);

  t.root.right = f;
  t.root.left = a;

  /*

         D
        / \
       /   \
      /     \
     A       F
  */

  a.right = b;
  a.left = e;

  f.right = t1;
  f.left = r;

  e.right = q;
  e.left = g;

  r.left = v;

  t1.right = l;
  t1.left = j;

  System.out.print("Preorder:\n");
  preorder(t.root);
  System.out.print("\nPostorder:\n");
  postorder(t.root);
  System.out.print("\nInorder:\n");
  inorder(t.root);
  System.out.print("\n");
}
}

So, you have learned a lot about binary trees in this chapter. We will always try to include more information in separate articles. You can check further readings or download the BlogsDope app to stay tuned.

Imagination is more important than knowledge

- Albert Einstein